вправа 4.40 гдз 10 клас алгебра Істер 2018
Вправа 4.40
Знайдіть функцію, обернену до функції:
1) у = х2 + 3, х ≥ 0; 2) у = х2 + 1, х ≤ 0; 3) у = х/(1+х); 4) у = √х-3, х ∈ [4; 12].
Знайдіть функцію, обернену до функції:
1) у = х2 + 3, х ≥ 0; 2) у = х2 + 1, х ≤ 0; 3) у = х/(1+х); 4) у = √х-3, х ∈ [4; 12].
Умова:
Відповідь:
1) у = х2 + 3, х ≥ 0
Функція у = х2 + 3 є оборотною на інтервалі [0; +∞),
тоді знайдемо обернену функцію
у - 3 = х2
х2 = у - 3
х = √у-3
Функція х2 ≥ 0, тоді і у - 3 ≥ 0.
Звідки у ≥ 3.
Для оберненної функції запишемо зручні позначення і отримаємо:
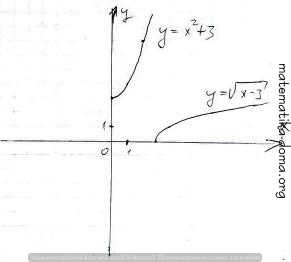
у = √х-3 при х ≥ 3
Функція у = х2 + 3 є оборотною на інтервалі [0; +∞),
тоді знайдемо обернену функцію
у - 3 = х2
х2 = у - 3
х = √у-3
Функція х2 ≥ 0, тоді і у - 3 ≥ 0.
Звідки у ≥ 3.
Для оберненної функції запишемо зручні позначення і отримаємо:
у = √х-3 при х ≥ 3
2) у = х2 + 1, х ≤ 0
Ця функція є оборотною на (-∞; 0], знайдемо обернену:
у = х2 + 1
х2 = у - 1, так як х2 ≥ 0, то у - 1 ≥ 0, тоді у ≥ 1
х = √у-1, згідно області визначення.
х ≤ 0, крім того √у-1 ≥ 0
при у ≥ 1 оберненної немає.













Коментування доступне тільки зареєстрованим
Будь ласка, увійдіть через Google, щоб залишити коментар.