вправа 12.42 гдз 10 клас геометрія Істер 2018
Вправа 12.42
Через вершину С квадрата ABCD проведено перпендикуляр СК завдовжки 6 см до його площини. Площини ABC і КВА утворюють між собою кут 45°. Знайдіть площу трикутника АКВ.
Через вершину С квадрата ABCD проведено перпендикуляр СК завдовжки 6 см до його площини. Площини ABC і КВА утворюють між собою кут 45°. Знайдіть площу трикутника АКВ.
Умова:
Відповідь - ГДЗ:
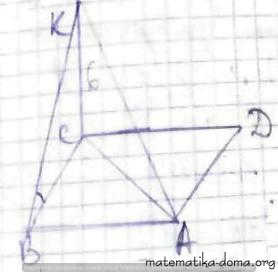
Нехай АВСD - квадрат,
СК ┴ АВСD, кут між АВС і КВА 45°.
Тобто ∠КВС = 45°.
Із ΔКСВ (∠КСВ = 90°) - рівнобедрений.
ВС = СК = 6 (см), КВ = 6√2 (см).
Тоді АВ = ВС = 6 (см)
АВСD - квадрат, тому АВ ┴ ВС, за теоремою
про три перпендикуляри АВ ┴ ВК,
тобто ΔАКВ - прямокутний.
SΔАКВ = 1/2 АВ • КВ = 1/2 • 6 • 6√2 = 18√2 (см2)
Відповідь: 18√2 см2













Коментування доступне тільки зареєстрованим
Будь ласка, увійдіть через Google, щоб залишити коментар.