вправа 12.73 гдз 10 клас геометрія Істер 2018
Вправа 12.73
ABCDA1B1C1D1 - куб, точка М - середина ребра В1С1, точка К - середина ребра CD, точка О - точка перетину діагоналей квадрата ABCD. Знайдіть кут між прямими: 1) А1М і ВК; 2) АВ1 і С1О.
ABCDA1B1C1D1 - куб, точка М - середина ребра В1С1, точка К - середина ребра CD, точка О - точка перетину діагоналей квадрата ABCD. Знайдіть кут між прямими: 1) А1М і ВК; 2) АВ1 і С1О.
Умова:
Відповідь - ГДЗ:
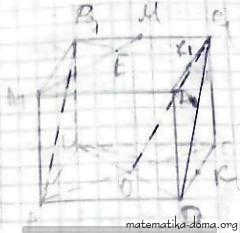
1) Кут між А1М і ВК дорівнює куту між А1М і В1К1
В1К1║ВК, В1К1 ⊂ (А1В1С1),
ΔА1ВС = ΔВ1С1К1 (за двома катетами).
Нехай А1М ∩ В1К1 = Е.
Позначимо ∠В1А1М = α,
∠А1МВ1 = β, тоді α + β = 90°.
Із того, що ΔА1В1М = ΔВ1С1К1 слідує ∠В1А1М = ∠К1В1С1 = α.
Розглянемо ΔВ1ЕМ, в ньому ∠ЕВ1М = α, ∠В1М1Е = β, тоді
∠В1ЕМ = 180° - (α + β) = 180° - 90° = 90°.
Отже, А1М ∩ В1К1 під кутом 90°,
тоді кут між А1М і ВС також 90°.
2) Проведемо С1D || АВ1, тоді кут між АВ1 і С1О
дорівнює куту між С1О і С1D, тобто це кут ∠ОС1D.
Нехай АВ = а - сторона куба,
С1D = а√2 - діагональ квадрата СС1D1D
ОD = 1/2 ВD = 1/2 • а√2 =
= а/√2 - половина діагоналі квадрата АВСD.
Знайдемо ОС1 із ΔОСС1, ∠ОСС1 = 90°
ОС = а√2, СС1 = а, тоді
ОС1 = √СС12+ОС2 = √а2+(а√2/2)2 = √3 а : √2.
Розглянемо ΔС1D:
cos∠ОС1D =
= (ОС12+С1D2-ОD2) : (2•ОС1•С1D)
cos∠ОС1D =
= (3/2 а2 + 2а2 - а2/2) : (2• (√3а/√2) • √2а)
cos∠ОС1D = (3/2 + 2 - 1/2) : 2√3
cos∠ОС1D = 3/2√3
cos∠ОС1D = √3/2
Тоді ∠ОС1D = arccos √3/2 = 30°.
Відповідь: 30°











