вправа 2.40 гдз 10 клас геометрія Істер 2018
Вправа 2.40
QABC - тетраедр, усі ребра якого по 4 см. Точки М і К -середини ребер AQ і BQ відповідно, точка Е належить ребру CQ, QE = 3 см. Знайдіть:
1) L1 - точку перетину прямої ME з площиною ABC;
2) L2 - точку перетину прямої КЕ з площиною ABC;
3) довжину відрізка L1L2;
4) точку перетину прямої ME з площиною АКС;
5) пряму перетину площин ML1K і L2QC;
6) у якому відношенні площина ML1L2 ділить відрізок QB, рахуючи від точки Q.
QABC - тетраедр, усі ребра якого по 4 см. Точки М і К -середини ребер AQ і BQ відповідно, точка Е належить ребру CQ, QE = 3 см. Знайдіть:
1) L1 - точку перетину прямої ME з площиною ABC;
2) L2 - точку перетину прямої КЕ з площиною ABC;
3) довжину відрізка L1L2;
4) точку перетину прямої ME з площиною АКС;
5) пряму перетину площин ML1K і L2QC;
6) у якому відношенні площина ML1L2 ділить відрізок QB, рахуючи від точки Q.
Умова:
Відповідь:
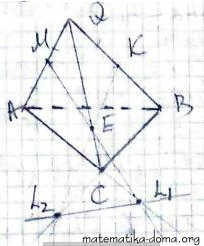1) МЕ ∩ АС = L1.Так як АС с (АВС), то L1 є (АВС).
2) КЕ ∩ ВС = L2.
Так як ВС с (АВС), то L2 є (АВС).
3) ΔQME = ΔQKE (QE - спільна, MQ = KQ, ∠MQE = ∠KQE), тому ∠QME = ∠MQE.
Тоді ∠AME = ∠ВКЕ, ΔAML1 = ΔBKL2 (АМ = ВС, ∠АМЕ = ∠ВКЕ, ∠МАС = ∠КВС),
тоді AL1 = BL2, отже L1 • CL1 = CL2.
Так як ∠АСВ = ∠L1CL2, то ΔL1CL2 - рівносторонній.
Із ΔMQE: МЕ2 = MQ2 + QE2 - 2MQ2 • QE2cos∠QME
ME2 = 4 + 9 - 2 • 2 • 3 • сos60°; МЕ = √7
Нехай CL1 = х, тоді AL1 = АЕ + CL1 = 4 + х
Із ΔЕСL1 за теоремою косинусів EL12 = EC2 + CL12 - 2 • EC • CL1cos∠ECL1;
∠ECL1 = 180° - ∠АСЕ = 180° - 90° = 120°.
EL12 = 1 + x2 - 2 • 1 • xcos120°; EL12 = 1 + x2 + x
ML1 = ME + EL1 = √7 + √1 + х2 + х
Із ΔAML за теоремою косинусів:
ML12 = AM2 + AL12 - 2 • AM • AL1cos∠MAL1
ML12 = 4 + (4 + x)2 - 2 • 2 • (4 + x)cos60°
ML12 = 4 + 16 + 8x + x2 - 8 - 2x
ML12 = x2 + 6x + 12, тоді ML1 = √х2 + 6х + 12.
Розв'яжемо рівняння:
√7 + √1 + х2 + х = √х2 + 6х + 12
(√7 + √1 + х2 + х)2 = х2 + 6х + 12
7 + 2√7(1 + х2 + х) + 1 + х2 + х = х2 + 6х + 12
2√7(1 + х2 + х) = 5х + 4
28(1 + х2 + х) = 25х2 + 40х + 16
3х2 - 12х + 12 = 0 | : 3
х2 - 4х + 4 = 0
х = 2, отже CL1 = 2 см.
Так як ΔL1CL2 рівносторонній, то L1L2 = CL1 = 2 см.
4) Так як L1 ∈ АС, АС с (АКС), то L1 ∈ (АКС).
З іншого боку L1 ∈ МЕ. Тому МЕ ∩ (АКС) = L1.
5) ML1 ⊂ (ML1K), Е ∈ ML1, тому Е ∈ (ML1K) і КЕ ⊂ (ML1K).
Так як К ∈ EL2, то KL2 ⊂ (ML1K), Е ∈ QC, QC ⊂ (L2QC), тому Е ∈ (L2QC).
Отже, EL2 ⊂ (L2QC).
Отже, (ML1K) ∩ (L2QC) = KL2.
6) KL2 ⊂ (ML1L2), QB ⊄ ML1L2,
KL2 ∩ QB = K, отже (ML1L2) ∩ QB = K.
Так як К - середина QB, то QK : КВ = 1 : 1.
Відповідь: 3) 2 см; 4) L1; 5) KL2; 6) 1 : 1.
