вправа 4.36 гдз 10 клас геометрія Істер 2018
Вправа 4.36
Трикутник ADF і ромб ABCD мають спільну сторону AD і лежать у різних площинах. Через сторону ВС і точку Р - середину DF - проведено площину, яка перетинає AF у точці Т.
1) Доведіть, що прямі AD і ТР паралельні.
2) Знайдіть ТР, якщо AD = 12 см.
3) Визначте вид чотирикутника ВТPC.
Трикутник ADF і ромб ABCD мають спільну сторону AD і лежать у різних площинах. Через сторону ВС і точку Р - середину DF - проведено площину, яка перетинає AF у точці Т.
1) Доведіть, що прямі AD і ТР паралельні.
2) Знайдіть ТР, якщо AD = 12 см.
3) Визначте вид чотирикутника ВТPC.
Умова:
Відповідь:
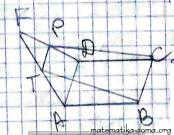ABCD - ромб, тоді AD║BC. За ознакою паралельності прямої і площини AD паралельна площині ВСР.
Нехай (ВСР) ∩ AF = Т, РТ ⊂ (ВСР).
Припустимо, що ТР ∩ AD = К, тоді AD ∩ (ВСР) = К, що протиречить тому,
що AD║(ВСР) (встановленному вище).
Отже, ТР║AD.
2) ТР ⊂ (ADF), ТР - середня лінія ΔADF, отже ТР = 1/2AD, ТР = 6 см.
3) Так як ТР - середня лінія ΔТР, то ТР║AD, ABCD - ромб, тоді ВС║AD.
За ознакою паралельності прямих ТР║ВС, причому ТР ≠ ВС, так як
ТР = 1/2AD, ВС = AD.
Тоді ВТРС - трапеція.
Відповідь: 2) 6 см; 3) трапеція.
