вправа 5.60 гдз 10 клас геометрія Істер 2018
Вправа 5.60
Площина β паралельна площині трикутника KLM. Світло, що виходить з точки Q, відкидає на площину β тінь K1L1M1 від трикутника KLM. Сторони трикутника K1L1M1 дорівнюють 12 см, 15 см, 9 см. Знайдіть:
1) сторони трикутника KLM, якщо QK : КК1 = 2 : 1;
2) площу трикутника KLM.
Площина β паралельна площині трикутника KLM. Світло, що виходить з точки Q, відкидає на площину β тінь K1L1M1 від трикутника KLM. Сторони трикутника K1L1M1 дорівнюють 12 см, 15 см, 9 см. Знайдіть:
1) сторони трикутника KLM, якщо QK : КК1 = 2 : 1;
2) площу трикутника KLM.
Умова:
Відповідь:
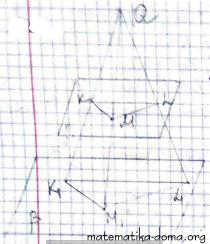Нехай ΔKLM лежить в площині α.
QK ∩ β = К1, QM ∩ β = М1, QL ∩ β = L1.
ΔК1М1L1 ⊂ β, QK : КК = 2 : 1, M1L1 = 12 см, К1М1 = 9 см, K1L1 = 15 см.
Знайдемо КМ, KL, ML, SΔKLM.
Розв'язання
Так як QK1 ∩ QM1 = Q, то проведемо площину γ через QK1 і QM1.
Площини KLM і β паралельні, тому γ ∩ (KLM) = КМ, γ ∩ β = К1М1.
За властивістю паралельних площин КМ║К1М1.
ΔQKM ~ ΔQK1M1 за двома кутами
(∠Q - спільний, ∠QKM = ∠QK1M1 - відповідні при паралельних прямих і січній).
Із подібності трикутників:
QK1/QK = K1M1/KM = QM1/QM
Нехай КК1 = х, тоді QK1 = QK + KK1 = 2x + x = 3x
3х/2х = К1М1/КМ; 3/2 = 9/КМ, звідки КМ = 6 (см).
Аналогічно можна довести, що ΔQML ~ ΔQM1L1, тоді
M1L1/ML = QM1/QM
M1L1/ML = 3/2; 12/ML = 3/2; ML = 8 (см)
Аналогічно можна довести, що ΔQKL ~ ΔQK1L1, тоді
K1L1/KL = QK1/QK
15/KL = 3/2; KL = 10 (см).
2) SΔKLM знайдемо за формулою Герона:
SΔ = √р • (р - а)(р - b)(р - с)
де р = 1/2(а + b + c)
р = 1/2(6 + 8 + 10) = 12
SΔ = √12 • 6 • 4 • 2 = 24 (см2).
Відповідь: 1) 6 см, 8 см, 10 см; 2) 24 см2