вправа 6.63 гдз 10 клас геометрія Істер 2018
Вправа 6.63
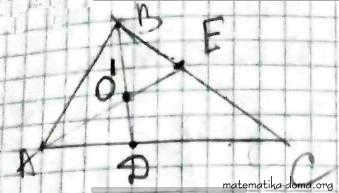
На даному зображенні трикутника зі сторонами 2, 3 і 4 побудуйте зображення центра кола, вписаного у трикутник.
На даному зображенні трикутника зі сторонами 2, 3 і 4 побудуйте зображення центра кола, вписаного у трикутник.
Умова:
Відповідь: Нехай т. О - центр вписаного кола в ΔА0В0С0.
Тоді т. О - точка перетину бісектрис цього трикутника,
А0В0 = 2 см, В0С0 = 3 см, А0С0 = 4 см.
Нехай В0D0, А0F0 - бісектриси ΔА0В0С0, т. О - А0Е0 ∩ B0D0.
За властивістю бісектриси трикутника:
A0D0/D0C0 = A0B0/B0C0, A0D0/D0C0 = 2/3
C0E0/B0E0 = A0C0/A0B0, С0Е0/В0Е0 = 4/2.
Нехай ΔАВС - зображення ΔА0В0С0.
AD/OC = A0D0/D0C0 = 2/3
СЕ/ВЕ = С0Е0/В0Е0 = 2.
Побудуємо точки D і Е і проведемо відрізки АЕ і BD.
Точка перетину відрізків АЕ і BD - є проекцією центра вписаного кола.