ТКР-2 гдз математика (геометрія) 10 клас Істер 2018
10 клас ➠ математика ➠ Істер
Тематично - контрольна робота № 2
Варіант 1
✔ 1. Пряма DМ проходить через вершину D прямокутника АВСD, DМ ┴ АD, DМ ┴ DС. Яким є взаємне розміщення прямої DМ і площини АВС?
DМ ┴ АD, DМ ┴ DС за ознакою перпендикулярності
прямої і площини DМ ┴ (АВСD).
Відповідь: В
✔ 2. Кожна з прямих CL і DM перпендикулярна до площини трикутника KLM. Яким є взаємне розміщення прямих CL і DM?
За властивість взаємоперпендикулярних прямих і площин CL║DM.
Відповідь: Б
✔ 3. З точки В до площини α проведено перпендикуляр ВТ і похилу BL. Тоді:
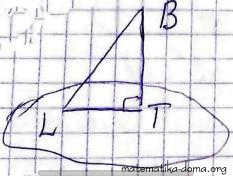
Відповідь: А
✔ 4. Пряма СМ перпендикулярна до площини прямокутника ABCD, АВ = 4 см, ВС = 3 см, АМ = 13 см. Знайдіть СМ.
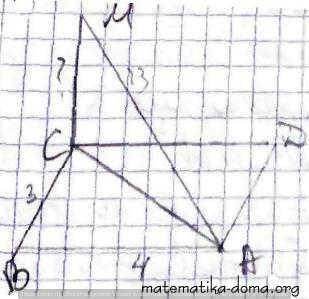
ΔАВС - прямокутний, ∠АВС = 90°,
АС2 = АВ2 + ВС2
АС = √АВ2+ВС2
АС = √32+42 = 5
ΔАСМ - прямокутний, ∠АСМ = 90°
СМ2 = АМ2 - АС2
СМ = √АМ2-АС2
СМ = √132-52 = √169-25 = 12 (см).
Відповідь: 12 см
✔ 5. З точки А до площини β проведено перпендикуляр АК та похилі АВ і АС, АВ = 15 см, ВК = 9 см, КС = 16 см. Знайдіть АС.
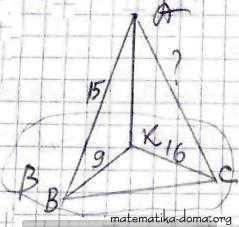
ΔАКВ і ΔАКС - прямокутні так,
як АК ┴ β, ∠АВК = 90°, ∠АКС = 90°.
Із ΔАКВ: АК = √АВ2-КВ2
АК = √152-92 = √225-81 = √144 = 12 (см)
Із ΔАКС, ∠К = 90°
АС = √АК2+КС2
АС = √144+256 = 20 (см).
Відповідь: 20 см
✔ 6. АК - перпендикуляр до площини прямокутного трикутника KMN, у якого ∠N = 90°. Доведіть, що AM ┴ NM.
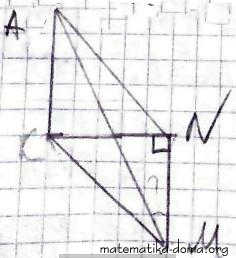
Доведемо, що AN ┴ NM.
ΔAKN - прямокутний, АК - перпендикуляр,
AN - похила, KN - проекція похилої.
Так, як ∠MNK = 90°, то MN ┴ KN,
за теоремою про три перпендикуляри MN ┴ AN.
✔ 7. Відрізок АВ завдовжки 17 см не має спільних точок із площиною γ. Прямі АС і BD перпендикулярні до площини γ і перетинають її у точках С і D. Знайдіть СD, якщо АС = 10 см, ВD = 2 см.
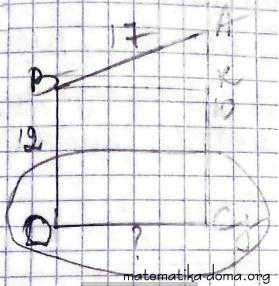
Так, як BD ┴ γ, АС ┴ γ, то за властивість
взаємноперпендикулярних прямих і площин АС║ВD.
Тоді АВСD - прямокутна трапеція.
Проведемо ВК║DС, ВК ┴ АС.
АК = АС - КС, КС = ВD так, як ВКСD - прямокутник,
тоді АК = 10 - 2 = 8 (см).
Із ΔАВК (∠К = 90°)
ВК = √АВ2-АК2
ВК = √172-82 = √289-64 = 15 (см)
СD = ВК = 15 (см) так, як ВКСD - прямокутник.
Відповідь: 15 см
✔ 8. Сторони трикутника дорівнюють 4 см, 13 см і 15 см. З вершини найбільшого кута до площини трикутника проведено перпендикуляр, і з другого його кінця до протилежної цьому куту сторони трикутника проведено перпендикуляр завдовжки 4 см. Знайдіть довжину перпендикуляра, проведеного до площини трикутника.
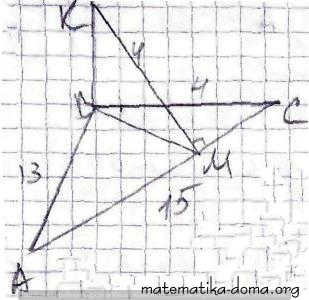
Нехай дано ΔАВС, АВ = 13 см, АС = 15 см, ВС = 4 см,
ВК ┴ АВС, КМ ┴ АС.
Знайдемо КВ.
Так, як КМ ┴ АС, то АС ┴ ВМ за теоремою про три перпендикуляри.
Отже, ВМ - висота ΔАВС, знайдемо ВМ.
SΔАВС = 1/2АС • ВМ
SΔАВС = √р(р-АВ)(р-АС)(р-ВС),
де р = 1/2(АВ + АС + ВС)
р = 1/2(13 + 4 + 15) = 16 (см)
SΔАВС = √16(16-13)(16-4)(16-15) =
= √16•3•12•1 = 24 (см2)
1/2 • 15 • ВМ = 24
ВМ = 3,2 (см)
Із ΔКВМ (∠В = 90°)
КВ = √КМ2-ВМ2
КВ = √16-10,24 = 2,4 (см)
Відповідь: 2,4 см
DМ ┴ АD, DМ ┴ DС за ознакою перпендикулярності
прямої і площини DМ ┴ (АВСD).
Відповідь: В
✔ 2. Кожна з прямих CL і DM перпендикулярна до площини трикутника KLM. Яким є взаємне розміщення прямих CL і DM?
За властивість взаємоперпендикулярних прямих і площин CL║DM.
Відповідь: Б
✔ 3. З точки В до площини α проведено перпендикуляр ВТ і похилу BL. Тоді:

Відповідь: А
✔ 4. Пряма СМ перпендикулярна до площини прямокутника ABCD, АВ = 4 см, ВС = 3 см, АМ = 13 см. Знайдіть СМ.

ΔАВС - прямокутний, ∠АВС = 90°,
АС2 = АВ2 + ВС2
АС = √АВ2+ВС2
АС = √32+42 = 5
ΔАСМ - прямокутний, ∠АСМ = 90°
СМ2 = АМ2 - АС2
СМ = √АМ2-АС2
СМ = √132-52 = √169-25 = 12 (см).
Відповідь: 12 см
✔ 5. З точки А до площини β проведено перпендикуляр АК та похилі АВ і АС, АВ = 15 см, ВК = 9 см, КС = 16 см. Знайдіть АС.

ΔАКВ і ΔАКС - прямокутні так,
як АК ┴ β, ∠АВК = 90°, ∠АКС = 90°.
Із ΔАКВ: АК = √АВ2-КВ2
АК = √152-92 = √225-81 = √144 = 12 (см)
Із ΔАКС, ∠К = 90°
АС = √АК2+КС2
АС = √144+256 = 20 (см).
Відповідь: 20 см
✔ 6. АК - перпендикуляр до площини прямокутного трикутника KMN, у якого ∠N = 90°. Доведіть, що AM ┴ NM.

Доведемо, що AN ┴ NM.
ΔAKN - прямокутний, АК - перпендикуляр,
AN - похила, KN - проекція похилої.
Так, як ∠MNK = 90°, то MN ┴ KN,
за теоремою про три перпендикуляри MN ┴ AN.
✔ 7. Відрізок АВ завдовжки 17 см не має спільних точок із площиною γ. Прямі АС і BD перпендикулярні до площини γ і перетинають її у точках С і D. Знайдіть СD, якщо АС = 10 см, ВD = 2 см.

Так, як BD ┴ γ, АС ┴ γ, то за властивість
взаємноперпендикулярних прямих і площин АС║ВD.
Тоді АВСD - прямокутна трапеція.
Проведемо ВК║DС, ВК ┴ АС.
АК = АС - КС, КС = ВD так, як ВКСD - прямокутник,
тоді АК = 10 - 2 = 8 (см).
Із ΔАВК (∠К = 90°)
ВК = √АВ2-АК2
ВК = √172-82 = √289-64 = 15 (см)
СD = ВК = 15 (см) так, як ВКСD - прямокутник.
Відповідь: 15 см
✔ 8. Сторони трикутника дорівнюють 4 см, 13 см і 15 см. З вершини найбільшого кута до площини трикутника проведено перпендикуляр, і з другого його кінця до протилежної цьому куту сторони трикутника проведено перпендикуляр завдовжки 4 см. Знайдіть довжину перпендикуляра, проведеного до площини трикутника.

Нехай дано ΔАВС, АВ = 13 см, АС = 15 см, ВС = 4 см,
ВК ┴ АВС, КМ ┴ АС.
Знайдемо КВ.
Так, як КМ ┴ АС, то АС ┴ ВМ за теоремою про три перпендикуляри.
Отже, ВМ - висота ΔАВС, знайдемо ВМ.
SΔАВС = 1/2АС • ВМ
SΔАВС = √р(р-АВ)(р-АС)(р-ВС),
де р = 1/2(АВ + АС + ВС)
р = 1/2(13 + 4 + 15) = 16 (см)
SΔАВС = √16(16-13)(16-4)(16-15) =
= √16•3•12•1 = 24 (см2)
1/2 • 15 • ВМ = 24
ВМ = 3,2 (см)
Із ΔКВМ (∠В = 90°)
КВ = √КМ2-ВМ2
КВ = √16-10,24 = 2,4 (см)
Відповідь: 2,4 см
