ТКР-5 гдз математика (геометрія) 10 клас Істер 2018
10 клас ➠ математика ➠ Істер
Тематично - контрольна робота № 5
✔ 1. Пряма m належить площині α, а пряма с перетинає площину α в точці, що не належить прямій m. Яке взаємне розміщення прямих m і с?
За ознакою мимобіжних прямих m і с - мимобіжні.
Відповідь: В ✔ 2. Точка L не належить площині β. Скільки можна провести прямих, які проходять через точку L і перпендикулярні до площини β?
Відповідь: Г
✔ 3. Знайдіть координати точки, що є серединою відрізка CD, якщо С(-2; 0; -5), D(6; 10; -1).
х0 = (-2+6)/3 = 2
у0 = (0+10)/2 = 5
z0 = (-5-1)/2 = -3
(2; 5; -3)
Відповідь: Б ✔ 4. ABCDA1B1C1D1 - прямокутний паралелепіпед. Укажіть:
1) пряму перетину площин ABD D1CC1;
2) площину, яка проходить через прямі BN і АА1. 1) АВD ∩ D1СС1 = СD
2) (АА1В1) ⊃ BN, (АА1В1) ⊃ АА1
Відповідь: 1) СD; 2) (АА1В1). ✔ 5. Двогранний кут дорівнює 45°. На одній з його граней дано точку, що віддалена на 8√2 см від другої грані. Знайдіть відстань від цієї точки ребра двогранного кута.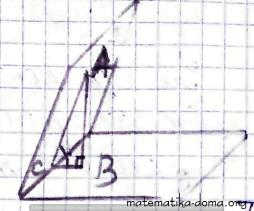
Нехай т. А належить грані двогранного кута.
АВ - відстань від т. А до другої грані.
АС - відстань від т. С до ребра кута,
∠АСВ = 45°, АВ = 8√2 см.
ΔАВС - прямокутний,
∠В = 90°, тоді ∠АСВ = ∠ВСА = 45°.
Отже, ΔАВС - рівнобедрений, тому АС = √(8√2)2+(8√)2 = 16 см.
Відповідь: 16 см ✔ 6. Дано: a (-2; 0; 3), b (4; -4; 2). Знайдіть:
1) координати вектораc = 2a - 3b ; 2) |c |. a (-2; 0; 3), b (4; -4; 2)
1) c = 2(-2; 0; 3) - 3(4; -4; 2) = (-4; 0; 6) - (12; -12; 6) = (-16; 12; 0);
2) |c | = √(-16)2+122 = 20. ✔ 7. Трикутник CDM і квадрат ABCD мають спільну сторону CD і лежать у різних площинах. Через сторону AB і точку N - середину відрізка CM - проведено площину, яка перетина DM у точці K.
1) Доведіть, що CD ║ NK;
2) знайдіть DC, якщо MK = 4 см;
3) визначте вид чотирикутника ABNK.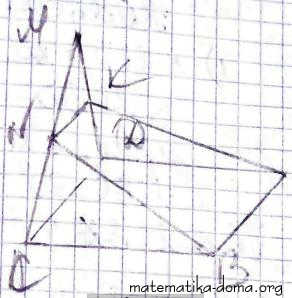
1) Так, як ABCD - квадрат, то СD║АВ, АВ ⊂ (АВN), СD ⊄ (АВN),
тоді СD║(АВN), (АВN) ∩ (СDN) = NК,
NК ⊂ (АВN), СD с (СDN), NК ⊂ (СDN), тоді СD║NК.
2) МК = 4 см
Так, як т. N - середина СМ, NK║CD
NК - середня лінія ΔСDМ,
тоді СD = 2NК = 2 • 4 = 8 см.
3) Так, як АВ║NK, BN непаралельно АК, то ABNK - трапеція.
Відповідь: 2) 8 см; 3) трапеція
За ознакою мимобіжних прямих m і с - мимобіжні.Відповідь: В ✔ 2. Точка L не належить площині β. Скільки можна провести прямих, які проходять через точку L і перпендикулярні до площини β?
Відповідь: Г
✔ 3. Знайдіть координати точки, що є серединою відрізка CD, якщо С(-2; 0; -5), D(6; 10; -1).
х0 = (-2+6)/3 = 2у0 = (0+10)/2 = 5
z0 = (-5-1)/2 = -3
(2; 5; -3)
Відповідь: Б ✔ 4. ABCDA1B1C1D1 - прямокутний паралелепіпед. Укажіть:
1) пряму перетину площин ABD D1CC1;
2) площину, яка проходить через прямі BN і АА1. 1) АВD ∩ D1СС1 = СD
2) (АА1В1) ⊃ BN, (АА1В1) ⊃ АА1
Відповідь: 1) СD; 2) (АА1В1). ✔ 5. Двогранний кут дорівнює 45°. На одній з його граней дано точку, що віддалена на 8√2 см від другої грані. Знайдіть відстань від цієї точки ребра двогранного кута.
Нехай т. А належить грані двогранного кута. АВ - відстань від т. А до другої грані.
АС - відстань від т. С до ребра кута,
∠АСВ = 45°, АВ = 8√2 см.
ΔАВС - прямокутний,
∠В = 90°, тоді ∠АСВ = ∠ВСА = 45°.
Отже, ΔАВС - рівнобедрений, тому АС = √(8√2)2+(8√)2 = 16 см.
Відповідь: 16 см ✔ 6. Дано: a (-2; 0; 3), b (4; -4; 2). Знайдіть:
1) координати вектораc = 2a - 3b ; 2) |c |. a (-2; 0; 3), b (4; -4; 2)
1) c = 2(-2; 0; 3) - 3(4; -4; 2) = (-4; 0; 6) - (12; -12; 6) = (-16; 12; 0);
2) |c | = √(-16)2+122 = 20. ✔ 7. Трикутник CDM і квадрат ABCD мають спільну сторону CD і лежать у різних площинах. Через сторону AB і точку N - середину відрізка CM - проведено площину, яка перетина DM у точці K.
1) Доведіть, що CD ║ NK;
2) знайдіть DC, якщо MK = 4 см;
3) визначте вид чотирикутника ABNK.
1) Так, як ABCD - квадрат, то СD║АВ, АВ ⊂ (АВN), СD ⊄ (АВN), тоді СD║(АВN), (АВN) ∩ (СDN) = NК,
NК ⊂ (АВN), СD с (СDN), NК ⊂ (СDN), тоді СD║NК.
2) МК = 4 см
Так, як т. N - середина СМ, NK║CD
NК - середня лінія ΔСDМ,
тоді СD = 2NК = 2 • 4 = 8 см.
3) Так, як АВ║NK, BN непаралельно АК, то ABNK - трапеція.
Відповідь: 2) 8 см; 3) трапеція
Коментування доступне тільки зареєстрованим
Будь ласка, увійдіть через Google, щоб залишити коментар.