гдз 10 клас математика Істер 2018 вправа 21.14
10 клас ➠ математика ➠ Істер
Вправа 21.14
Умова: Знайдіть критичні точки функції:
1) g(x) = х + 2cosx; 2) f(x) = (3+х2)/(х+1).
Відповідь:
1) g(x) = x + 2cosx, Д(g) = R
g '(x) = 1 - 2sinx
g '(x) = 0: 1 - 2sinx = 0
-2sinx = -1
sinx = 1/2
x = (-1)n arcsin1/2 + πn, n є Z
х = (-1)nπ/6 + πn, n є Z; 2) f(x) = (3+x2)/(x+1), Д(f): x ≠ 1
f '(x) = ((3+x2)'(x+1)-(x+1)'(3+x2))/(x+1)2 = (2x(x+1)-(3+x2))/(x+1)2 =
= (2x2+2x-3-x2)/(x+1)2 = (x2+2x-3)/(x+1)2
f '(x) = 0: x2 + 2x - 3 = 0
х1 + х2 = -3 х1 = -3
{
х1 • х2 = -3 х2 = 1.
Умова: Знайдіть критичні точки функції:
1) g(x) = х + 2cosx; 2) f(x) = (3+х2)/(х+1).
Відповідь:
1) g(x) = x + 2cosx, Д(g) = R
g '(x) = 1 - 2sinx
g '(x) = 0: 1 - 2sinx = 0
-2sinx = -1
sinx = 1/2
x = (-1)n arcsin1/2 + πn, n є Z
х = (-1)nπ/6 + πn, n є Z; 2) f(x) = (3+x2)/(x+1), Д(f): x ≠ 1
f '(x) = ((3+x2)'(x+1)-(x+1)'(3+x2))/(x+1)2 = (2x(x+1)-(3+x2))/(x+1)2 =
= (2x2+2x-3-x2)/(x+1)2 = (x2+2x-3)/(x+1)2
f '(x) = 0: x2 + 2x - 3 = 0
х1 + х2 = -3 х1 = -3
{
х1 • х2 = -3 х2 = 1.
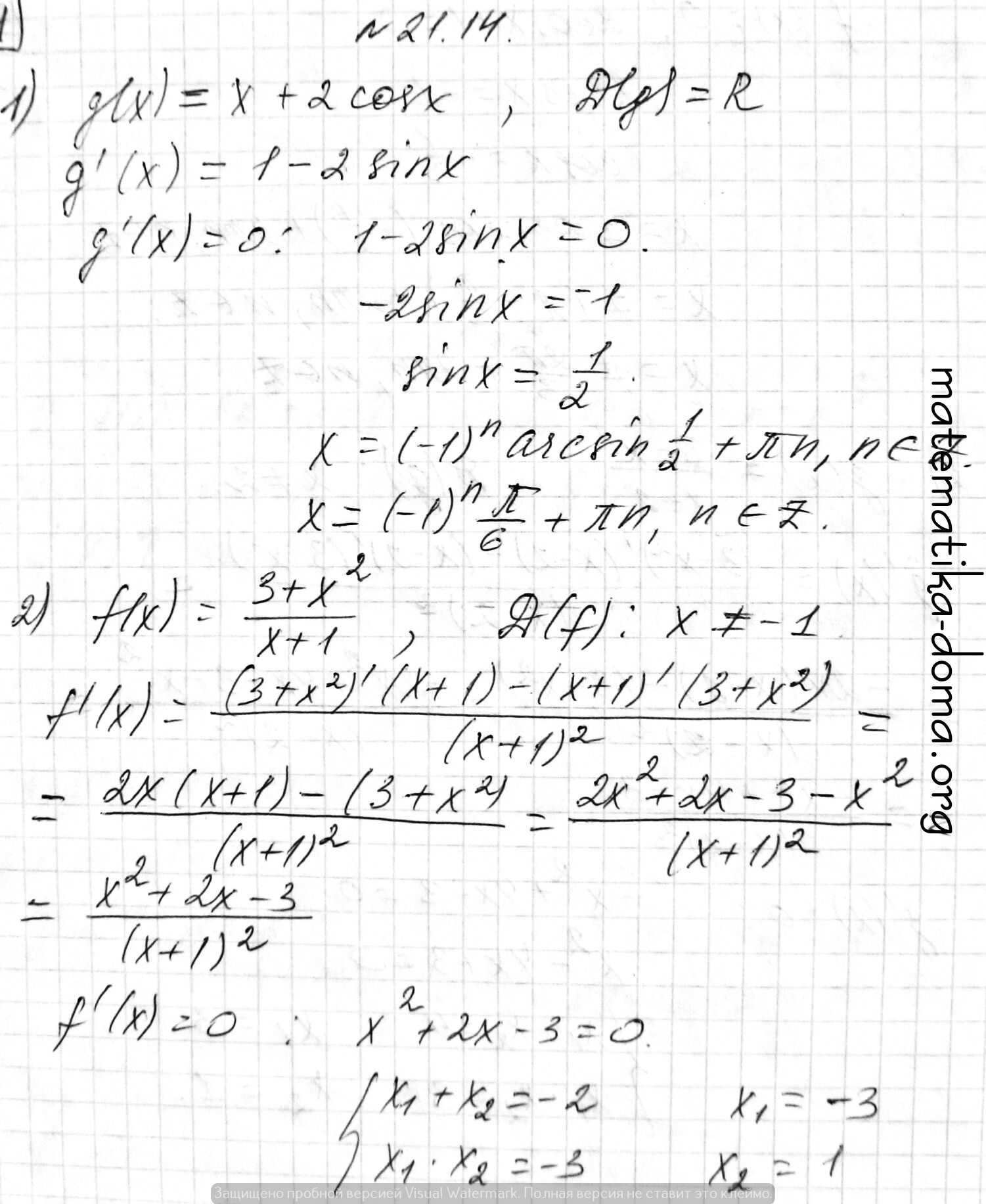













Коментування доступне тільки зареєстрованим
Будь ласка, увійдіть через Google, щоб залишити коментар.