ГДЗ Алгебра 11 клас домашня самостійна робота №1 Істер 2019
Домашня самостійна робота № 1
1 № 1
Умова:
Порівняйте а і b, якщо 0,7а > 0,7b.
А. а ≥ b Б. а > b В. а < b Г. а = b
А. а ≥ b Б. а > b В. а < b Г. а = b
Відповідь: В.
a, b - ? 0,7a > 0,7b
В. а < b
В. а < b
№ 2
Умова:
Розв'яжіть рівняння 5х+2 = 125.
А. 3 Б. 1 В. -1 Г. 5
А. 3 Б. 1 В. -1 Г. 5
Відповідь: Б.
5х+2 = 125
х + 2 = 3
5х+2 = 53
х = 3 - 2 = 1
х = 1.
Б. 1
х + 2 = 3
5х+2 = 53
х = 3 - 2 = 1
х = 1.
Б. 1
№ 3
Умова:
Укажіть множину розв'язків нерівності (1/7)х < (1/7)3.
А. [3; +∞) Б. (3; +∞) В. (-∞; 3] Г. (-∞; 3)
А. [3; +∞) Б. (3; +∞) В. (-∞; 3] Г. (-∞; 3)
Відповідь: А.
(1/7)х < (1/7)3 1/7 < 1 =>
x ≥ 3
А. х є [3; +∞)
x ≥ 3
А. х є [3; +∞)
2 № 4
Умова:
Укажіть функцію, що зростає на R.
А. у = 1х Б. у = 0,1х В. у = (1/π)х Г. πх
А. у = 1х Б. у = 0,1х В. у = (1/π)х Г. πх
Відповідь: Г.
у ↑
Г. у = πх
Г. у = πх
№ 5
Умова:
Розв'яжіть рівняння 2х+3 - 2х = 56.
А. 2 Б. 8 В. 3 Г. 0
А. 2 Б. 8 В. 3 Г. 0
Відповідь: В.
2х+3 - 2х = 56
2х • 23 - 2х = 56
2х • (8 - 1) = 56
2х • 7 = 56
2х = 56/7
2х = 8
2х = 23
х = 3
В. х = 3
2х • 23 - 2х = 56
2х • (8 - 1) = 56
2х • 7 = 56
2х = 56/7
2х = 8
2х = 23
х = 3
В. х = 3
№ 6
Умова:
Розв'яжіть нерівність (1/9)-2х ≤ 27
А. (-∞; 3/4] Б. [3/4; +∞) В. (-∞; -3/4] Г. [-3/4; +∞)
А. (-∞; 3/4] Б. [3/4; +∞) В. (-∞; -3/4] Г. [-3/4; +∞)
Відповідь: А.
(1/9)-2х ≤ 27
(3-2)-2x ≤ 33
34x ≤ 33
4x ≤ 3
x ≤ 3/4
А. х є (-∞; 3/4]
(3-2)-2x ≤ 33
34x ≤ 33
4x ≤ 3
x ≤ 3/4
А. х є (-∞; 3/4]
3 № 7
Умова:
Знайдіть значення виразу 16√3-1 • 43-2√3
А. 16 Б. 5 В. 0,25 Г. 1.
А. 16 Б. 5 В. 0,25 Г. 1.
Відповідь: А.
16√3-1 • 43-2√3
42√3-1 • 43-2√3 = 42√3-1+3-2√3 = 42 = 16
А. 16
42√3-1 • 43-2√3 = 42√3-1+3-2√3 = 42 = 16
А. 16
№ 8
Умова:
Знайдіть область визначення функції у = √9х - 3х-1
А. [-1; +∞) Б. (-1; +∞) В. [1; +∞) Г. (-∞; +∞)
А. [-1; +∞) Б. (-1; +∞) В. [1; +∞) Г. (-∞; +∞)
Відповідь: А.
у = √9х - 3х-1 ОВФ - ?
9х - 3х-1 ≥ 0
32x - 3x • 3-1 ≥ 0
32x - 3x • 1/3 ≥ 0
3 • 32x - 3x ≥ 0
3x(3 • 3x - 1) ≥ 0
3x ≥ 0 3 • 3x - 1 ≥ 0
х є R 3 • 3x ≥ 1
3x ≥ 1/3 3x ≥ 3-1
x ≥ -1
А. х є [-1; +∞)
9х - 3х-1 ≥ 0
32x - 3x • 3-1 ≥ 0
32x - 3x • 1/3 ≥ 0
3 • 32x - 3x ≥ 0
3x(3 • 3x - 1) ≥ 0
3x ≥ 0 3 • 3x - 1 ≥ 0
х є R 3 • 3x ≥ 1
3x ≥ 1/3 3x ≥ 3-1
x ≥ -1
А. х є [-1; +∞)
№ 9
Умова:
Укажіть множину коренів рівняння 32х+1 + 2 • 3х+1 - 9 = 0.
А. Ø Б. -1; 0 В. 1; 0 Г. 0
А. Ø Б. -1; 0 В. 1; 0 Г. 0
Відповідь: Г.
32х+1 + 2 • 3х+1 - 9 = 0
32х • 31 + 2 • 3х • 31 - 9 = 0
заміна: 3х = t, t > 0
3t2 + 6t - 9 = 0 : 3
t2 + 2t - 3 = 0
Д = 4 - 4 • (-3) = 16
t1;2 = (-2±4)/2, t1 = -3 не підходить, t2 = 1
3х = t2
3x = 1
3x = 30
x = 0
Г. х = 0
32х • 31 + 2 • 3х • 31 - 9 = 0
заміна: 3х = t, t > 0
3t2 + 6t - 9 = 0 : 3
t2 + 2t - 3 = 0
Д = 4 - 4 • (-3) = 16
t1;2 = (-2±4)/2, t1 = -3 не підходить, t2 = 1
3х = t2
3x = 1
3x = 30
x = 0
Г. х = 0
4 № 10
Умова:
Скільки розв'язків має рівняння (1/6)х = -6/х?
А. жодного Б. один В. два Г. безліч
А. жодного Б. один В. два Г. безліч
Відповідь: Б.
(1/6)х = -6/х
графічним способом
у = (1/6)х
у = -6/х
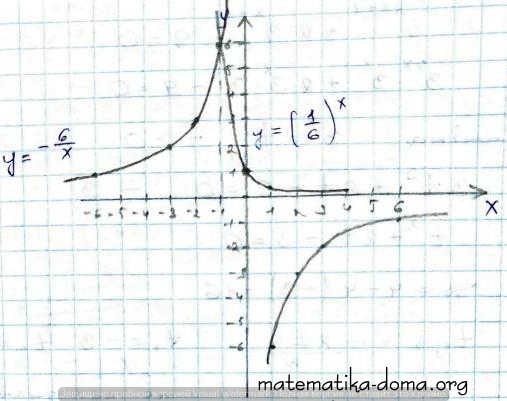
графічним способом
у = (1/6)х
| х | -1 | 0 | 1 |
| у | 6 | 1 | 1/6 |
| х | -6 | -3 | -2 | 2 | 3 | 6 |
| у | 1 | 2 | 3 | -3 | -2 | -1 |
рівняння має 1 розв'язок
№ 11
Умова:
Знайдіть усі корені рівняння (3√2 - √3)х + (3√2 + √3)х = 4.
А. З Б. -6; 6 В. -3; З Г. -1; 1
А. З Б. -6; 6 В. -3; З Г. -1; 1
Відповідь: В.
(3√2 - √3)х + (3√2 + √3)х = 4
3√2 - √3 • 3√2 + √3 = 3√(2 - √3)(2 + √3) = 3√4 - 3 = 3√1 = 1
=> 3√2 - √3 = 1/(3√2 + √3)
нехай:
(3√2 + √3)х = t, t > 0
(3√2 - √3)х = 1/t
t + 1/t - 4 = 0
t2 - 4t + 1 = 0
Д = (-4)2 - 4 = 16 - 4 = 12
√Д = √12 = 2√3
t1;2 = (4±2√3)/2 = (2(2±√3))/2 = 2±√3
(3√2 + √3)х = 2 + √3 (3√2 + √3)х = 2 - √3
(2 + √3)х/3 = 2 + √3 (2 + √3)х/3 = 1/(2 + √3)
х/3 = 1 (2 + √3)х/3 = (2 + √3)-1
х = 3 х/3 = -1
х = -3
В. 3; -3
3√2 - √3 • 3√2 + √3 = 3√(2 - √3)(2 + √3) = 3√4 - 3 = 3√1 = 1
=> 3√2 - √3 = 1/(3√2 + √3)
нехай:
(3√2 + √3)х = t, t > 0
(3√2 - √3)х = 1/t
t + 1/t - 4 = 0
t2 - 4t + 1 = 0
Д = (-4)2 - 4 = 16 - 4 = 12
√Д = √12 = 2√3
t1;2 = (4±2√3)/2 = (2(2±√3))/2 = 2±√3
(3√2 + √3)х = 2 + √3 (3√2 + √3)х = 2 - √3
(2 + √3)х/3 = 2 + √3 (2 + √3)х/3 = 1/(2 + √3)
х/3 = 1 (2 + √3)х/3 = (2 + √3)-1
х = 3 х/3 = -1
х = -3
В. 3; -3
№ 12
Умова:
Розв'яжіть нерівність 2 • 2х + 2х + 2х-1 ≤ 6x-1 + 6x.
А. [0; +∞) Б. [1; +∞) В. (-∞; 1] Г. [-1; +∞)
А. [0; +∞) Б. [1; +∞) В. (-∞; 1] Г. [-1; +∞)
Відповідь: Б.
2 • 2х + 2х + 2х-1 ≤ 6x-1 + 6x
2 • 2x + 2x + 2x • 2-1 ≤ 6x • 6-1 + 6x
2 • 2x + 2x + 2x/2 ≤ 6x/6 + 6x
12 • 2x + 6 • 2x + 3 • 2x ≤ 6x + 6 • 6x
21 • 2x ≤ 7 • 6x : 6x
(21 • 2x)/(7 • 6x) ≤ 1
3 • (2/6)x ≤ 1
(2/6)x ≤ 1/3
(1/3)x ≤ 1/3
x ≥ 1
Б. х є [1; +∞)
2 • 2x + 2x + 2x • 2-1 ≤ 6x • 6-1 + 6x
2 • 2x + 2x + 2x/2 ≤ 6x/6 + 6x
12 • 2x + 6 • 2x + 3 • 2x ≤ 6x + 6 • 6x
21 • 2x ≤ 7 • 6x : 6x
(21 • 2x)/(7 • 6x) ≤ 1
3 • (2/6)x ≤ 1
(2/6)x ≤ 1/3
(1/3)x ≤ 1/3
x ≥ 1
Б. х є [1; +∞)
Домашня самостійна робота №1 з алгебри 11 класу Істер 2019 на Matematika-doma. Готові відповіді до всіх завдань.
