вправа 13.20 гдз 11 клас алгебра Істер 2019
Вправа 13.20
Побудуйте фігуру, площа якої дорівнює даному інтегралу, та обчисліть її площу:
4
1) ∫ (2х - 1)dx;
1
2
2) ∫ (х2 + 2х)dx.
1
4
1) ∫ (2х - 1)dx;
1
2
2) ∫ (х2 + 2х)dx.
1
Умова:
Відповідь ГДЗ:
4
✔ 1) ∫ (2х - 1)dx
1
фігура:
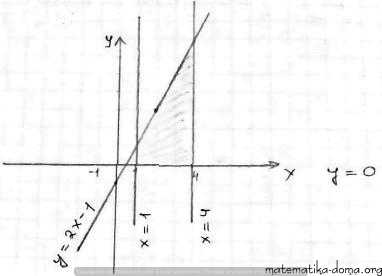
4
Sф = ∫ (2х - 1)dx =
1
4 4 4 4
= 2х2/2 | - х | = х2 | - х | =
1 1 1 1
= 42 - 1 - 4 + 1 = 16 - 4 = 12
Sф = 12;
2
✔ 2) ∫ (х2 + 2х)dx
1
фігура:
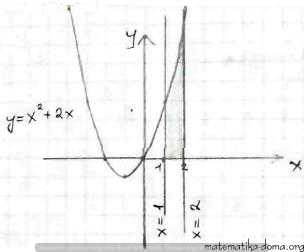
2 2 2
Sф = ∫ (х2 + 2х)dx = х3/3 | + 2х2/2 | =
1 1 1
= 23/3 - 13/3 + 22 - 12 = 8/3 - 1/3 + 4 - 1 =
= 7/3 + 3 = 2 1/3 + 3 = 5 1/3
Sф = 5 1/3.
✔ 1) ∫ (2х - 1)dx
1
фігура:
4
Sф = ∫ (2х - 1)dx =
1
4 4 4 4
= 2х2/2 | - х | = х2 | - х | =
1 1 1 1
= 42 - 1 - 4 + 1 = 16 - 4 = 12
Sф = 12;
2
✔ 2) ∫ (х2 + 2х)dx
1
фігура:
2 2 2
Sф = ∫ (х2 + 2х)dx = х3/3 | + 2х2/2 | =
1 1 1
= 23/3 - 13/3 + 22 - 12 = 8/3 - 1/3 + 4 - 1 =
= 7/3 + 3 = 2 1/3 + 3 = 5 1/3
Sф = 5 1/3.