вправа 15.49 гдз 11 клас алгебра Істер 2019

у = sinх, у = х² - πх, Sф - ?



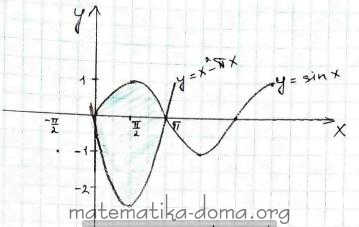
у = х² - πх
х² - πх = 0
х(х - π) = 0
х₁ = 0, х₂ = π
х₀ = π/2
у₀ = π²/4 - π²/2 = -2,5
(π/2; -2,5) - вершина
             π                 π
Sф = ∫sinхdx - ∫(х² - πх)dx =
            0                  0
    π                  π               π
= ∫sinхdx - ∫х²dx + ∫πхdx =
    0                  0                0
                 π              π                  π
= -cosх | - х³/3 | + πх²/2 | =
                 0              0                   0
= -cosπ + cos0 - π³ : 3 + 0/3 +
+ (π•π²) : 2 - 0/2 = -(-1) + 1 -
- π³/3 + π²/2 = 2 + π³/6 = 2 + 5,16 = 7,16
Sф = 7,16.