вправа 3.38 гдз 11 клас алгебра Істер 2019
Вправа 3.38
Умова:
Розв'яжіть нерівність:
1) 2 • 4х - 5 • 6х + 3 • 9х ≥ 0;
2) 5 • 4х + 2 • 25х < 7 • 10х.
1) 2 • 4х - 5 • 6х + 3 • 9х ≥ 0;
2) 5 • 4х + 2 • 25х < 7 • 10х.
Відповідь:
1) 2 • 4х - 5 • 6х + 3 • 9х ≥ 0
6х = 2х • 3х
2 • 22х - 5 • 2х • 3х + 3 • 32х ≥ 0 : 32х
32x ≠ 0
(2•22х)/32х - (5•2х•3х)/32х + (3•22х)/32х ≥ 0
2 • (2/3)2х - 5 • (2/3)х + 3 ≥ 0
(2/3)х = t, t > 0
2t2 - 5t + 3 ≥ 0
Д = (-5)2 - 4 • 2 • 3 = 1
t1;2 = (5±1)/4, t1 = 1, t2 = 3/2
1 ≤ t ≤ 3/2
(2/3)x ≥ 1 (2/3)x ≤ 3/2
(2/3)x ≥ (2/3)0 (2/3)x ≤ (2/3)-1
функція у = (2/3)t x ≥ -1
є спадною, =>
x ≤ 0

х є [-∞; -1] U [0; +∞);
6х = 2х • 3х
2 • 22х - 5 • 2х • 3х + 3 • 32х ≥ 0 : 32х
32x ≠ 0
(2•22х)/32х - (5•2х•3х)/32х + (3•22х)/32х ≥ 0
2 • (2/3)2х - 5 • (2/3)х + 3 ≥ 0
(2/3)х = t, t > 0
2t2 - 5t + 3 ≥ 0
Д = (-5)2 - 4 • 2 • 3 = 1
t1;2 = (5±1)/4, t1 = 1, t2 = 3/2
1 ≤ t ≤ 3/2
(2/3)x ≥ 1 (2/3)x ≤ 3/2
(2/3)x ≥ (2/3)0 (2/3)x ≤ (2/3)-1
функція у = (2/3)t x ≥ -1
є спадною, =>
x ≤ 0

х є [-∞; -1] U [0; +∞);
2) 5 • 4х + 2 • 25х < 7 • 10х
10х = 2х • 5х
5 • 22х + 2 • 52х < 7 • 2х • 5х : 52х
52х ≠ 0
(5•22х)/52х + (2•52х)/52х < (7•2х•5х)/52х
5 • (2/5)2х + 2 < 7 • (2/5)х
(2/5)х = t, t > 0
5t2 - 7t + 2 < 0
Д = (-7)2 - 5 • 4 • 2 = 9
t1;2 = (7±3)/10, t1 = 2/5, t2 = 1
2/5 < t < 1
(2/5)х > 2/5 (2/5)х < 1
функція у = (2/5)t є спадною, =>
x > 1 x > 0
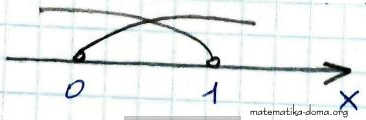
х є (0; 1).
10х = 2х • 5х
5 • 22х + 2 • 52х < 7 • 2х • 5х : 52х
52х ≠ 0
(5•22х)/52х + (2•52х)/52х < (7•2х•5х)/52х
5 • (2/5)2х + 2 < 7 • (2/5)х
(2/5)х = t, t > 0
5t2 - 7t + 2 < 0
Д = (-7)2 - 5 • 4 • 2 = 9
t1;2 = (7±3)/10, t1 = 2/5, t2 = 1
2/5 < t < 1
(2/5)х > 2/5 (2/5)х < 1
функція у = (2/5)t є спадною, =>
x > 1 x > 0

х є (0; 1).













