вправа 7.56 гдз 11 клас алгебра Істер 2019
Вправа 7.56
Розв'яжіть нерівність методом інтервалів:
1) (4х2 - 8х - 5)log3(х + 1) < 0;
2) (х2 - 3)lgх2 - хlgх4 ≥ 0.
1) (4х2 - 8х - 5)log3(х + 1) < 0;
2) (х2 - 3)lgх2 - хlgх4 ≥ 0.
Умова:
Відповідь:
1) (4х2 - 8х - 5)log3(х + 1) < 0
ОДЗ: х + 1 > 0, х > -1
4х2 - 8х - 5 = 0
{
log3(х + 1) = 0 - знаходимо нулі функції
4х2 - 8х - 5 = 0
Д = (-8)2 - 4 • 4 • (-5) = 64 + 80 = 144
х1;2 = (8±12)/8 = 2,5; -0,5
log3(х + 1) = 0
х + 1 = 30
х + 1 = 1
х = 0
ОДЗ: х + 1 > 0, х > -1
4х2 - 8х - 5 = 0
{
log3(х + 1) = 0 - знаходимо нулі функції
4х2 - 8х - 5 = 0
Д = (-8)2 - 4 • 4 • (-5) = 64 + 80 = 144
х1;2 = (8±12)/8 = 2,5; -0,5
log3(х + 1) = 0
х + 1 = 30
х + 1 = 1
х = 0
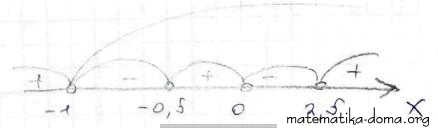
х ∈ (-1; -0,5) U (0; 2,5);
2) (х2 - 3)lgх - 4хlgх ≥ 0
ОДЗ: х > 0
lgх(2(х2 - 3) - 4х) ≥ 0
lgх = 0
{ } нулі функції
(2(х2 - 3) - 4х = 0
х = 100
{
2х2 - 6 - 4х = 0 : 2
х = 1
{
х2 - 2х - 3 = 0
Д = (-2)2 - 4 • (-3) = 16
х1;2 = (2±4)/2 = 3; -1
х = -1 - не підходить під ОДЗ
2) (х2 - 3)lgх - 4хlgх ≥ 0
ОДЗ: х > 0
lgх(2(х2 - 3) - 4х) ≥ 0
lgх = 0
{ } нулі функції
(2(х2 - 3) - 4х = 0
х = 100
{
2х2 - 6 - 4х = 0 : 2
х = 1
{
х2 - 2х - 3 = 0
Д = (-2)2 - 4 • (-3) = 16
х1;2 = (2±4)/2 = 3; -1
х = -1 - не підходить під ОДЗ
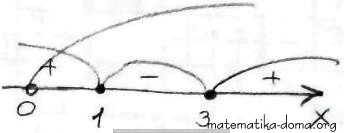
х ∈ (0; 1] U [3; +∞).













