вправа 10.56 гдз 11 клас геометрія Істер 2019
Вправа 10.56
У правильній трикутній зрізаній піраміді сторони основ дорівнюють 6 см і 3 см, а бічне ребро нахилене до площини основи під кутом 60°. Знайдіть об'єм зрізаної піраміди.
Умова:
Відповідь ГДЗ:
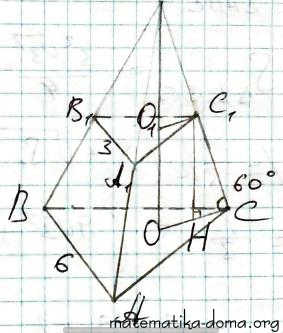Дано:
ΔАВС - рівносторонній
ΔА1В1С1 - рівносторонній
А1В1 = 3 см
АВ = 6 см
∠НСС1 = 60°
Знайти V.
Розв'язання:
ОС - радіус, описаного кола нижньої основи,
а О1С - радіус описаного кола верхньої основи.
ОС = а√3/3 = 6√3/3 = 2√3 (см)
О1С1 - а√3/3 = 3√3/3 = √3 (см)
НС = ОС - О1С1 = 2√3 - √3 = √3 (см)
Із ΔС1НС
tg60° = С1Н/СН
h = С1Н = СН • tg60° = √3 • √3 = 3 (см)
SΔАВС = а2√3 : 4 = 62√3 : 4 = 9√3 (см2)
SΔА1В1С1 = 32√3 : 4 = 9/4 √3 (см2)
V = 1/3 • h • (S1 + √S1•S2 + S2) =
= 1/3 • 3 • (9√3 + √9√3•(9√4):4 + 9/4 √3) =
= 9√3/2 + 9/4 √3 + 9√3 =
= 18√3/4 + 9√3/4 + 36√3/4 = 63√3 : 4 (см3)
Відповідь: 63√3 : 4 см3
Дано:ΔАВС - рівносторонній
ΔА1В1С1 - рівносторонній
А1В1 = 3 см
АВ = 6 см
∠НСС1 = 60°
Знайти V.
Розв'язання:
ОС - радіус, описаного кола нижньої основи,
а О1С - радіус описаного кола верхньої основи.
ОС = а√3/3 = 6√3/3 = 2√3 (см)
О1С1 - а√3/3 = 3√3/3 = √3 (см)
НС = ОС - О1С1 = 2√3 - √3 = √3 (см)
Із ΔС1НС
tg60° = С1Н/СН
h = С1Н = СН • tg60° = √3 • √3 = 3 (см)
SΔАВС = а2√3 : 4 = 62√3 : 4 = 9√3 (см2)
SΔА1В1С1 = 32√3 : 4 = 9/4 √3 (см2)
V = 1/3 • h • (S1 + √S1•S2 + S2) =
= 1/3 • 3 • (9√3 + √9√3•(9√4):4 + 9/4 √3) =
= 9√3/2 + 9/4 √3 + 9√3 =
= 18√3/4 + 9√3/4 + 36√3/4 = 63√3 : 4 (см3)
Відповідь: 63√3 : 4 см3
