вправа 11.42 гдз 11 клас геометрія Істер 2019
Вправа 11.42
Умова:
У циліндрі, паралельно його осі, проведено площину, що перетинає основу по хорді, яку видно із центра цієї основи під кутом 60°. Площа перерізу, що при цьому утворився, дорівнює 12√3 см2, а кут між діагоналлю перерізу і твірною циліндра дорівнює 60°. Знайдіть об'єм циліндра.
Відповідь ГДЗ:
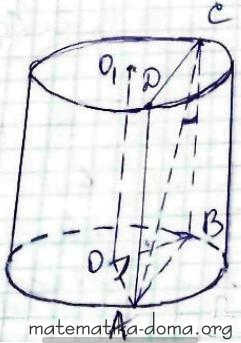Нехай АВСD - переріз паралельний
осі ОО1 циліндра, ∠АОВ = 60°,
∠АСВ = 60°, SАВСD = 12√3 см2.
Знайдемо V - об'єм циліндра.
Нехай h - висота циліндра, тоді СВ = h.
Із ΔАВС (∠АВС = 90°)
АВ = СВ = tg∠АСВ = htg60° = h√3.
Тоді SАВСD = АВ • СВ = h2√3,
за умовою SАВСD = 12√3, тому
h2√3 = 12√3, звідки h = 2√3 (см).
Тоді АВ = 2√3 • √3 = 6 (см).
ΔАОВ - рівносторонній так, як
АО = ВО = R - радіуси циліндра ∠АОВ = 60°.
Отже, АО = АВ = 6 (см).
V = πR2h = π • АО2 • h =
π • 62 • 2√3 = 72√3 π (см3).
Відповідь: 72√3 π см3
Нехай АВСD - переріз паралельний осі ОО1 циліндра, ∠АОВ = 60°,
∠АСВ = 60°, SАВСD = 12√3 см2.
Знайдемо V - об'єм циліндра.
Нехай h - висота циліндра, тоді СВ = h.
Із ΔАВС (∠АВС = 90°)
АВ = СВ = tg∠АСВ = htg60° = h√3.
Тоді SАВСD = АВ • СВ = h2√3,
за умовою SАВСD = 12√3, тому
h2√3 = 12√3, звідки h = 2√3 (см).
Тоді АВ = 2√3 • √3 = 6 (см).
ΔАОВ - рівносторонній так, як
АО = ВО = R - радіуси циліндра ∠АОВ = 60°.
Отже, АО = АВ = 6 (см).
V = πR2h = π • АО2 • h =
π • 62 • 2√3 = 72√3 π (см3).
Відповідь: 72√3 π см3
