вправа 13.58 гдз 11 клас геометрія Істер 2019
Вправа 13.58
Умова:
Умова:
Висота правильної трикутної піраміди дорівнює 1 см, а бічне ребро - 4 см. Знайдіть об'єм кулі, описаної навколо цієї піраміди.
Відповідь ГДЗ:
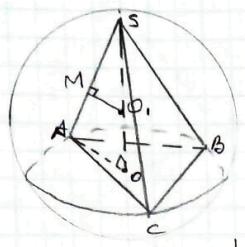 Дано:
Дано:
куля, описана навколо піраміди SACB
SО = 1 см
SА = 4 см
Знайти: Vк. - ?
Розв'язання:
Куля, описана навколо
правильної 3-∠ піраміди. \begin{equation} V_{K.}=\frac{4}{3}\Pi R^{3} \end{equation} В ΔAOS ∠SOA = 90°
АО - радіус кола, описаного навколо ΔАВС.
За теоремою Піфагора: \begin{equation} AO=\sqrt{SA^{2}-SO^{2}}= \end{equation} \begin{equation} AO=\sqrt{4^{2}-1}=\sqrt{15} \end{equation} В ΔAOS О1М - середини ┴ \begin{equation} AM=MS=\frac{SA}{2}= \end{equation} \begin{equation} =\frac{4}{2}=2(CM) \end{equation} В ΔМО1S О1М ┴ АS
ΔАSО ~ ΔМО1S \begin{equation} \frac{SA}{SM}=\frac{4}{2}=k \end{equation} k = 2 \begin{equation} \frac{AS}{O_{1}S}=k \end{equation} \begin{equation} O_{1}S=\frac{AS}{k} \end{equation} \begin{equation} O_{1}S=\frac{4}{2}=2 \end{equation} O1S = k кулі \begin{equation} V_{K.}=\frac{4}{2}\Pi \cdot 8= \end{equation} \begin{equation} =\frac{32}{3}\Pi (CM^{3}). \end{equation}
 Дано:
Дано:куля, описана навколо піраміди SACB
SО = 1 см
SА = 4 см
Знайти: Vк. - ?
Розв'язання:
Куля, описана навколо
правильної 3-∠ піраміди. \begin{equation} V_{K.}=\frac{4}{3}\Pi R^{3} \end{equation} В ΔAOS ∠SOA = 90°
АО - радіус кола, описаного навколо ΔАВС.
За теоремою Піфагора: \begin{equation} AO=\sqrt{SA^{2}-SO^{2}}= \end{equation} \begin{equation} AO=\sqrt{4^{2}-1}=\sqrt{15} \end{equation} В ΔAOS О1М - середини ┴ \begin{equation} AM=MS=\frac{SA}{2}= \end{equation} \begin{equation} =\frac{4}{2}=2(CM) \end{equation} В ΔМО1S О1М ┴ АS
ΔАSО ~ ΔМО1S \begin{equation} \frac{SA}{SM}=\frac{4}{2}=k \end{equation} k = 2 \begin{equation} \frac{AS}{O_{1}S}=k \end{equation} \begin{equation} O_{1}S=\frac{AS}{k} \end{equation} \begin{equation} O_{1}S=\frac{4}{2}=2 \end{equation} O1S = k кулі \begin{equation} V_{K.}=\frac{4}{2}\Pi \cdot 8= \end{equation} \begin{equation} =\frac{32}{3}\Pi (CM^{3}). \end{equation}













