вправа 5.31 гдз 11 клас геометрія Істер 2019
Вправа 5.31
Діагональ перерізу циліндра, який паралельний його осі, дорівнює 12 см і утворює з площиною основи кут 60°. Переріз відтинає від кола основи дугу в 60°. Знайдіть:
1) висоту циліндра;
2) площу перерізу циліндра;
3) радіус циліндра;
4) довжину кола основи.
1) висоту циліндра;
2) площу перерізу циліндра;
3) радіус циліндра;
4) довжину кола основи.
Умова:
Відповідь:
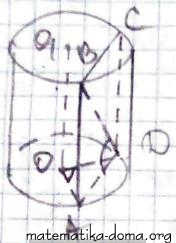
Нехай задано циліндр, ОО1 - висота циліндра,
ABCD - переріз, паралельний до ОО1, BD = 12 см, ∠BDA = 60°, ∠AOD = 60°.
1) Із ΔABD (∠А = 90°), АВ = BDsin∠BDA = 12sin60° = 12 √3/2 = 6√3 (см) - висота циліндра;
2) ABCD - прямокутник, тому SABCD = AB • AD
Із ΔАВD, AD = BDcosBDA = 12cos60° = 6 (см), тоді SABCD = 6√3 • 6 = 36√3 (см2);
3) ΔAOD - рівностороній, так як АО = DO = R, ∠AOD = 60°, тоді АО = AD = 6 (см);
4) l = 2πR, l = 2π • 6 = 12π (см).
Відповідь: 1) 6√3 см; 2) 36√3 см2; 3) 6 см; 4) 12π см