вправа 6.36 гдз 11 клас геометрія Істер 2019
Вправа 6.36
Висота конуса дорівнює 3√2 см і утворює з твірною кут 45°. Через дві твірні конуса, що утворюють між собою кут 60°, проведено площину. Знайдіть відстань від центра основи конуса до хорди, по якій площина перерізу перетинає площину основи конуса.
Умова:
Відповідь:
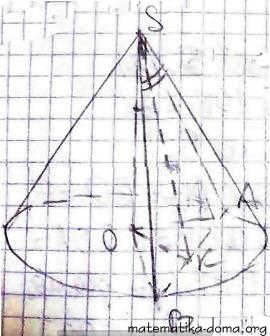
Нехай S - вершина конуса, АВ - хорда, SО - висота, SО = 3√2 см.
∠ОSВ = 45°, ∠АSВ = 60°.
Знайдемо ОК - відстань від центра основи до хорди
по еній площина перетинає основу конуса
ΔSОВ - прямокутнийю, ∠SОВ = 90°, тоді
SВ = SО/sin∠ОSВ
SВ = 3√2/sin45° = 6 (см)
ΔАSВ - рівнобедрений і ∠АSВ = 60°,
тому ΔАSВ - рівносторонній.
Отже, АВ = SВ = 6 (см)
SК - висота і медіана ΔАSВ, тому із ΔSКВ (∠SКВ = 90°)
SК2 = SВ2 - ВК2
ВК = 1/2АВ = 3 см
SК2 = 62 - 32 = 36 - 9 = 27
Із ΔSОК (∠SОК = 90°)
ОК = √SК2-SО2
ОК = √27-(3√2)2 = √27-18 = 9 (см).
Відповідь: 9 см