вправа 9.27 гдз 11 клас геометрія Істер 2019
Вправа 9.27
Бічне ребро прямокутного паралелепіпеда дорівнює 4√3 см, а діагональ основи - 20 см. Знайдіть об'єм паралелепіпеда, якщо одна з діагоналей бічної грані нахилена до площини основи під кутом 30°.
Умова:
Відповідь ГДЗ:
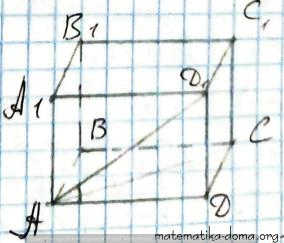Дано:
DD1 = 4√3 см
АС = 20 см
∠D1АD = 30°
Знайти Vп - ? см3
tg30° = DD1 : AD => tg30° = 4√3 : АD
AD = 4√3 : 1/√3 = 4 • 3 = 12 см
Із ΔАDС знайдемо СD за теоремою Піфагора:
СD = √202-122 = 16 см
V = Sосн. • h = 12 • 16 • 4√3 = 768√3 (см3).
Відповідь: V = 768√3 см3
Дано:DD1 = 4√3 см
АС = 20 см
∠D1АD = 30°
Знайти Vп - ? см3
tg30° = DD1 : AD => tg30° = 4√3 : АD
AD = 4√3 : 1/√3 = 4 • 3 = 12 см
Із ΔАDС знайдемо СD за теоремою Піфагора:
СD = √202-122 = 16 см
V = Sосн. • h = 12 • 16 • 4√3 = 768√3 (см3).
Відповідь: V = 768√3 см3
