вправа 1.16 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 1.16
Умова:
Висота прямої призми дорівнює 15, її основою є рівнобічна трапеція з висотою 10 і основами 25 і 45. Знайдіть:
1) площу бічної поверхні призми;
2) площу діагонального перерізу призми;
3) двогранні кути при бічних ребрах призми.
1) площу бічної поверхні призми;
2) площу діагонального перерізу призми;
3) двогранні кути при бічних ребрах призми.
Розв'язання:
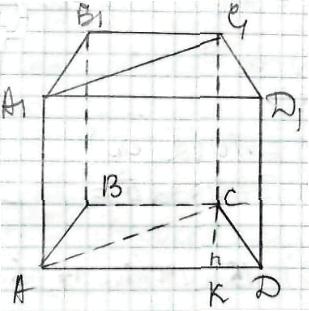
Нехай ABCDA1B1C1D1 - пряма призма,
АВСD - рівнобічна трапеція.
СК - висота трапеції,
АС - діагональ трапеції,
АА1С1С - діагональний переріз призми.
1) Sбіч. = Р • h, де Р - периметр основи призми h - висота.
Так як призма пряма, то бічне ребро АА1 є висотою призми.
Так як АВСD - рівнобічна трапеція,
СК - її висота, то \begin{equation} KD=\frac{AD-BC}{2}= \end{equation} \begin{equation} =\frac{45-25}{2}=10 (од.) \end{equation} Із ΔСКD (∠СКD = 90°) \begin{equation} CD=\sqrt{CK^{2}+KD^{2}} \end{equation} \begin{equation} CD=\sqrt{10^{2}+10^{2}}= \end{equation} \begin{equation} =10\sqrt{2}(од.).\end{equation} Тоді Р = 10√2 + 10√2 + 45 + 25 =
= 20√2 + 70
Sбіч. = (20√2 + 70) • 15 =
= 150(2√2 + 7) (кв.од.).
2) АА1С1С - діагональний переріз призми.
Так як АВСDА1В1С1D1 - пряма призма,
то АА1С1С - прямокутник.
SАА1С1С = АА1 • АС
АК = АD - КD = 45 - 10 = 35 (од.)
Із ΔАСК (∠АКС = 90°) \begin{equation} AC=\sqrt{AK^{2}+CK^{2}} \end{equation} \begin{equation} AC=\sqrt{10^{2}+35^{2}}= \end{equation} \begin{equation} =5\sqrt{53} \end{equation} \begin{equation} S_{AA_{}C_{1}C}=15\cdot 5\sqrt{53}= \end{equation} \begin{equation} =75\sqrt{53}(кв.од.). \end{equation} 3) Так як DD1 ┴ (АВС),
то DD1 ┴ СD і DD1 ┴ АD,
тому ∠АDС - лінійний кут двогранного кута при ребрі DD1.
Величина двогранного кута відповідно тоді дорівнює величині кута АDС.
Із ΔСКD (∠СКD = 90°)
СК = 10, КD = 10,
тоді ΔСКD - рівнобедрений,
отже ∠АDС = ∠КDС = \begin{equation} =\frac{1}{2}(180^{\circ}-90^{\circ})=45^{\circ}. \end{equation} Аналогічно доводиться, що ∠ВСD - лінійний кут двогранного кута при ребрі СС1, тоді його величина ∠ВСD = 180° - ∠КDС =
= 180° - 45° = 135°.
Відповідь: \begin{equation} 1)150(2\sqrt{2}+7) кв.од.; \end{equation} \begin{equation} 2)75\sqrt{53} кв.од.; \end{equation} \begin{equation} 3)45^{\circ} та 135^{\circ} \end{equation}