вправа 12.9 гдз 11 клас математика (геометрія) Нелін Долгова 2019

Вправа 12.9


Умова: 

Конус вписано в кулю. Радіус основи конуса дорівнює радіусу кулі, об'єм конуса дорівнює 6 куб. од. Знайдіть об'єм кулі.

Розв'язання:


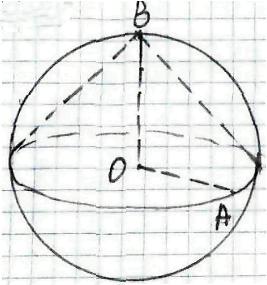
Нехай конус вписано в кулю з центром в т.О.
ОА = R - радіус основи конуса, за умовою радіус кулі теж ОА.
Так як радіуси основи конуса і кулі однакові, то основа конуса є великим колом кулі.
Тоді висота конуса ОВ дорівнює радіусу кулі,
тобто ОВ = ОА = R.
Отже об'єм конуса: \begin{equation} V_{к.}=\frac{1}{3}\Pi R^{2}\cdot OB= \end{equation} \begin{equation} =\frac{1}{3}\Pi R^{2}\cdot R=\frac{1}{3}\Pi R^{3}, \end{equation} за умовою V_к. = 6, тоді \begin{equation} \frac{1}{3}\Pi R^{3}=6 куб. од. \end{equation} Об'єм кулі: \begin{equation} V=\frac{4}{3}\Pi R^{3}, \end{equation} тоді \begin{equation} V=4\cdot \frac{1}{3}\Pi R^{3}= \end{equation} = 4 • 6 = 24 (куб. од.)
Відповідь: 24 куб. од.