вправа 2.2 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 2.2
Умова:
Сторони основи прямокутного паралелепіпеда дорівнюють 7 дм і 24 дм, а висота паралелепіпеда 8 дм. Знайдіть площу діагонального перерізу.
Розв'язання:
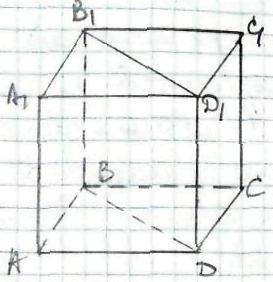Нехай ABCDA1B1C1D1 - прямокутний паралелепіпед,
тоді ВВ1 і DD1 перпендикулярні основам паралелепіпеда і є висотами.
АВСD і А1В1С1D1 - рівні прямокутники.
Із ΔАВD (∠ВАD = 90°)
АВ = 7 дм,
АD = 24 дм \begin{equation} BD=\sqrt{AB^{2}+AD^{2}} \end{equation} \begin{equation} BD=\sqrt{7^{2}+24^{2}}= \end{equation} \begin{equation} BD=\sqrt{625}=25 (дм) \end{equation} ВВ1D1D - прямокутник, діагональний переріз паралелепіпеда.
SВВ1D1D = ВD • ВВ1;
SВВ1D1D = 25 • 8 = 200 (дм2).
Відповідь: 200 дм2
Нехай ABCDA1B1C1D1 - прямокутний паралелепіпед, тоді ВВ1 і DD1 перпендикулярні основам паралелепіпеда і є висотами.
АВСD і А1В1С1D1 - рівні прямокутники.
Із ΔАВD (∠ВАD = 90°)
АВ = 7 дм,
АD = 24 дм \begin{equation} BD=\sqrt{AB^{2}+AD^{2}} \end{equation} \begin{equation} BD=\sqrt{7^{2}+24^{2}}= \end{equation} \begin{equation} BD=\sqrt{625}=25 (дм) \end{equation} ВВ1D1D - прямокутник, діагональний переріз паралелепіпеда.
SВВ1D1D = ВD • ВВ1;
SВВ1D1D = 25 • 8 = 200 (дм2).
Відповідь: 200 дм2
