вправа 2.8 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 2.8
Умова:
Знайдіть площу бічної поверхні прямокутного паралелепіпеда, якщо його висота дорівнює h, площа основи Q, площа діагонального перерізу М.
Розв'язання:
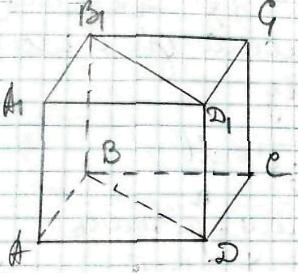
Нехай ABCDA1B1C1D1 - прямокутний паралелепіпед,
тоді АВСD - прямокутник, бічні ребра перпендикулярні основам паралеелпіпеда,
ВВ1D1D - діагональний переріз - прямокутник.
Позначимо АВ = а, АD = b, тоді
Sбіч. = Росн. • h = 2(а + b) • h
Sосн. = а • b, за умовою
Sосн. = Q, тобто, аb = Q.
Із ΔАВD (∠ВАD = 90°) \begin{equation} BD=\sqrt{a^{2}+b^{2}} \end{equation} З іншого боку ВВ1D1D - прямокутник, тому \begin{equation} BD=\frac{S_{BB_{1}D_{1}D}}{h}, \end{equation} де SВВ1D1D = М (за умовою) - площа діагонального перерізу, тому \begin{equation} BD=\frac{M}{h}. \end{equation} Отже, \begin{equation} \sqrt{a^{2}+b^{2}}=\frac{M}{h}. \end{equation} Маємо систему рівнянь: \begin{equation} \left\{\begin{matrix} ab=Q & \\ \sqrt{a^{2}+b^{2}}=\frac{M}{h} & \end{matrix}\right. \end{equation} \begin{equation} \left\{\begin{matrix} ab=Q & \\ a^{2}+b^{2}=(\frac{M}{h})^{2} & \end{matrix}\right. \end{equation} \begin{equation} \left\{\begin{matrix} 2ab=2Q & \\ a^{2}+2ab+b^{2}=\\=(\frac{M}{h})^{2}+2Q & \end{matrix}\right. \end{equation} \begin{equation} \left\{\begin{matrix} 2ab=2Q & \\ (a^{2}+b^{2})=\\=(\frac{M}{h})^{2}+2Q & \end{matrix}\right. \end{equation} Із системи знайдемо а + b: \begin{equation} a+b= \end{equation} \begin{equation} =\sqrt{\frac{M^{2}}{h^{2}}+2Q} \end{equation} \begin{equation} a+b= \end{equation} \begin{equation} =\sqrt{\frac{M^{2}+2Qh^{2}}{h}} \end{equation} Тоді Sбіч. = 2(а + b) • h = \begin{equation} =2\cdot \sqrt{\frac{M^{2}+2Qh^{2}}{h}}\cdot h= \end{equation} \begin{equation} =2\sqrt{M^{2}+2Qh^{2}}. \end{equation} Відповідь: \begin{equation} 2\sqrt{M^{2}+2Qh^{2}} \end{equation}