вправа 3.13 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 3.13
Умова:
Через діагональ основи правильної чотирикутної призми проведено переріз, паралельний діагоналі призми. Знайдіть площу перерізу, якщо висота призми дорівнює 4 см, а сторона її основи 2 см.
Розв'язання:
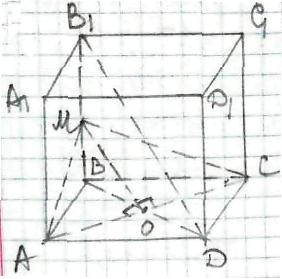
АВСDА1В1С1D1 - правильна призма,
бічні ребра перпендикулярні основам призми і є висотами,
тому ВВ1 = 4 см.
АВСD - квадрат,
АВ = ВС = СD = АD = 2 см
АС ┴ ВD і АС ∩ ВD = О,
АО = ОС = ВО = ОD.
Нехай перетин проходе через АС.
Проведемо ОМ║В1D.
Отже, перетин АМС проходе через АС і перетинає ВВ1 в точці М.
МО ┴ АС за теоремою про три перпендикуляри.
Тоді площу перерізу АМС можна знайти: \begin{equation} S_{\Delta AMC}=\frac{1}{2}AC\cdot MO \end{equation} Так як АВСD квадрат,
то АС = ВD = АВ√2 (см)
Із ΔВВ1D (∠ВВ1D = 90°) \begin{equation} tg\angle BDB_{1}=\frac{BB_{1}}{BD}= \end{equation} \begin{equation} =\frac{4}{2\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2} \end{equation} Знайдемо cos∠ВDВ1, скориставшись формулою: \begin{equation} tg^{2}\varphi +1=\frac{1}{cos^{2}\varphi }, \end{equation} тоді \begin{equation} cos\angle BDB_{1}= \end{equation} \begin{equation} =\sqrt{\frac{1}{tg^{2}\angle BDB_{1}+1}}= \end{equation} \begin{equation} =\sqrt{\frac{1}{(\sqrt{2})^{2}+1}}= \end{equation} \begin{equation} =\frac{1}{\sqrt{3}}. \end{equation} Так як ∠ВDВ1 = ∠МОВ, то \begin{equation} cos\angle MOB=\frac{1}{\sqrt{3}} \end{equation} Із ΔМВО (∠МВО = 90°) \begin{equation} MO=\frac{BO}{cos\angle MOB}= \end{equation} \begin{equation} =\sqrt{2}\cdot \sqrt{3}=\sqrt{6} \end{equation} \begin{equation} S_{\Delta AMC}=\frac{1}{2}AC\cdot MO= \end{equation} \begin{equation} =\frac{1}{2}\cdot 2\sqrt{2}\cdot \sqrt{6}= \end{equation} \begin{equation} =2\sqrt{3} (см^{2}). \end{equation} \begin{equation} Відповідь: 2\sqrt{3} см^{2} \end{equation}