вправа 3.14 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 3.14
Умова:
У правильній трикутній призмі, кожне ребро якої дорівнює а, побудуйте переріз, що проходить через сторону основи й середину відрізка, який сполучає центри основ. Знайдіть площу перерізу і кут між площиною перерізу й площиною основи.
Розв'язання:
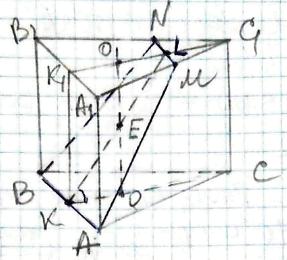
АВСА1В1С1 - правильна призма,
кожне ребро якої а.
Нехай ОО1 - відрізок, що сполучає центри
АВС і А1В1С1 основ призми,
К і К1 - середина АВ і А1В1.
Перетином площини АВЕ (т.Е - середина ОО1)
з А1В1С1 є відрізок MN.
Так як (АВС)║(А1В1С1),
то MN || АВ і, відповідно, MN║А1В1.
Так як С1К ┴ А1В1,
А1В1 ┴ MN,
то С1К1 ┴ MN.
ΔLК1К - прямокутний (∠LК1К = 90°)
LК1 - проекція LК на А1В1С1,
то із того, що С1К1 ┴ МN слідує,
що МN ┴ LК (за теоремою при три перпендикуляри).
Отже, тоді з того, що МN║АВ, слідує,
що LК ┴ АВ.
З іншого боку СК - висота ΔАВС,
тоді ∠LКС - кут між перерізом АВNМ
і площиною АВС основи призми.
ΔАВС - рівносторонній, тому \begin{equation} CK=\frac{\sqrt{3}}{2}AB= \end{equation} \begin{equation} =\frac{\sqrt{3}}{2}a \end{equation} Так як т.О - центр ΔАВС, то \begin{equation} OK=\frac{1}{3}CK= \end{equation} \begin{equation} =\frac{\sqrt{3}}{6}a \end{equation} т.Е - середина ОО, тоді \begin{equation} OE=\frac{1}{2}OO_{1}=\frac{1}{2}a \end{equation} Із ΔЕОК (∠ЕОК = 90°) \begin{equation} tg\angle EKO=\frac{EO}{OK}= \end{equation} \begin{equation} =\frac{\frac{1}{2}a}{\frac{\sqrt{3}}{6}a}=\frac{3}{\sqrt{3}}=\sqrt{3}, \end{equation} тоді ∠ЕКО = 60°.
Отже, ∠LКС = ∠ЕКО = 60°.
Так як MN || AB,
то АВNМ - трапеція, LК - її висота.
Знайдемо \begin{equation} S_{пер.}=S_{ABNM}= \end{equation} \begin{equation} =\frac{1}{2}(AB+MN)\cdot LK. \end{equation} Знайдемо спочатку МN, для цього розглянемо ΔА1В1С1.
В ньому О1К = ОК,
О1L = ОК (із ΔЕО1L = ΔЕОК),
тоді LК1 = 2OК
Так як С1К1 = СК = 3OК,
то С1L = 3 • ОК - 2 • ОК = ОК
ΔА1В1С1 ~ ΔМNС (за двома кутами),
тоді \begin{equation} \frac{A_{1}B_{1}}{MN}=\frac{C_{1}K_{1}}{C_{1}L}= \end{equation} \begin{equation} =\frac{3OK}{OK}=3 \end{equation} Отже, \begin{equation} MN=\frac{A_{1}B_{1}}{3} \end{equation} \begin{equation} MN=\frac{a}{3} \end{equation} Із ΔЕОК (∠ЕОК = 90°) \begin{equation} KE=\sqrt{EO^{2}+OK^{2}}= \end{equation} \begin{equation} =\sqrt{\frac{1}{4}a^{2}+(\frac{\sqrt{3}}{6}a)^{2}}= \end{equation} \begin{equation} =\sqrt{\frac{1}{4}a^{2}+\frac{3}{36}a^{2}}= \end{equation} \begin{equation} =\sqrt{\frac{4a^{2}}{12}}=\frac{a}{\sqrt{3}} \end{equation} \begin{equation} LK=2KE=\frac{2a}{\sqrt{3}} \end{equation} \begin{equation} S_{пер.}=\frac{1}{2}(AB+MN)\cdot LK= \end{equation} \begin{equation} =\frac{1}{2}(a+\frac{a}{3})\cdot \frac{2a}{\sqrt{3}}= \end{equation} \begin{equation} =\frac{1}{2}\cdot \frac{4a}{3}\cdot \frac{2a}{\sqrt{3}}= \end{equation} \begin{equation} =\frac{4a^{2}}{3\sqrt{3}}=\frac{4a^{2}\sqrt{3}}{9}. \end{equation} \begin{equation} Відповідь: \frac{4a^{2}\sqrt{3}}{9}; 60^{\circ} \end{equation}