вправа 3.5 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 3.5
Умова:
У прямій трикутній призмі через сторону основи під кутом 45° до неї проведено площину, що перетинає протилежне бічне ребро. Знайдіть площу перерізу, якщо площа основи дорівнює Q.
Розв'язання:
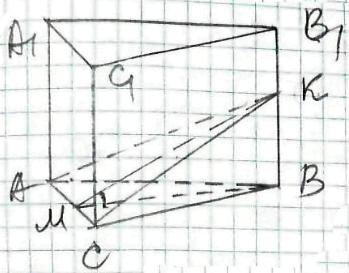
АВСА1В1С1 - пряма призма.
Бічні ребра перпендикулярні основам і є висотами призми,
зокрема СС1 ┴ (АВС).
ΔАКС - переріз, що проходе через ребро АС під кутом 45° до площини (АВС).
Тоді ΔАВС - ортогональна проекція ΔАКС,
тоже SΔАВС = SΔАКСcosφ,
де φ = 45° - кут між (АКС) і (АВС).
Звідки: \begin{equation} S_{\Delta AKC}=\frac{S_{\Delta ABC}}{cos\varphi } \end{equation} \begin{equation} S_{\Delta AKC}=\frac{Q}{cos45^{\circ}} \end{equation} \begin{equation} S_{\Delta AKC}=\frac{Q}{\frac{\sqrt{2}}{2}}= \end{equation} \begin{equation} =\frac{2Q}{\sqrt{2}}=Q\sqrt{2}. \end{equation} \begin{equation} Відповідь: Q\sqrt{2} \end{equation}

АВСА1В1С1 - пряма призма.
Бічні ребра перпендикулярні основам і є висотами призми,
зокрема СС1 ┴ (АВС).
ΔАКС - переріз, що проходе через ребро АС під кутом 45° до площини (АВС).
Тоді ΔАВС - ортогональна проекція ΔАКС,
тоже SΔАВС = SΔАКСcosφ,
де φ = 45° - кут між (АКС) і (АВС).
Звідки: \begin{equation} S_{\Delta AKC}=\frac{S_{\Delta ABC}}{cos\varphi } \end{equation} \begin{equation} S_{\Delta AKC}=\frac{Q}{cos45^{\circ}} \end{equation} \begin{equation} S_{\Delta AKC}=\frac{Q}{\frac{\sqrt{2}}{2}}= \end{equation} \begin{equation} =\frac{2Q}{\sqrt{2}}=Q\sqrt{2}. \end{equation} \begin{equation} Відповідь: Q\sqrt{2} \end{equation}













