вправа 3.7 гдз 11 клас математика (геометрія) Нелін Долгова 2019

11 клас ➠ математика ➠ Нелін Долгова

 

Вправа 3.7


Умова: 

 

Основою прямої трикутної призми АВСА1В1С1 є рівнобедрений трикутник ABC,
де АВ = ВС = 25 см, АС = 30 см. Через бічне ребро АА1 призми проведено площину, перпендикулярну до ребра ВС. Визначте висоту призми, якщо площа утвореного перерізу дорівнює 72 см².

 

Розв'язання:



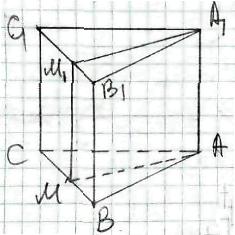АВСА1В1С1 - пряма призма,
бічне ребро АА1 перпендикулярне до площини основи (АВС),
АВ = ВС = 25 см,
АС = 30 см.
Проведемо АМ ┴ ВС,
так як АА1 ┴ (АВС),
то АМ ┴ АА1.
Основи призми паралельні,
побудуємо А1М1║АМ і
сполучимо точки М і М1.
Тоді АММ1А1 - переріз.
Враховуючи, що АА1 ∩ ММ1,
АМ║А1М,
АА1 ┴ АМ
маємо, що АММ1А1 - прямокутник.
SАММ₁А₁ = 72 см².
Знайдемо АА1 - висоту призми.
Знайдемо за формулою Герона: \begin{equation} S_{\Delta ABC}= \end{equation} \begin{equation} =\sqrt{p(p-a)(p-b)(p-c)} \end{equation} \begin{equation} p=\frac{1}{2}(25+ \end{equation} \begin{equation} +25+30)=40 \end{equation} \begin{equation} S_{ABC}= \end{equation} \begin{equation} =\sqrt{40\cdot 15\cdot 15\cdot 10}= \end{equation} \begin{equation} =300 (см^{2}) \end{equation} З іншого боку \begin{equation} S_{ABC}=\frac{1}{2}AM\cdot BC \end{equation} \begin{equation} \frac{1}{2}AM\cdot 25=300, \end{equation} звідки АМ = 24.
Тоді \begin{equation} AA_{1}=\frac{S_{AMM_{1}A_{1}}}{AM}= \end{equation} \begin{equation} =\frac{72}{24}=3 (см). \end{equation} Відповідь: 3 см