вправа 4.15 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 4.15
Умова:
Центр однієї з граней куба і середини сторін протилежної грані є вершинами піраміди. Знайдіть площу бічної поверхні піраміди, якщо ребро куба дорівнює а.
Розв'язання:
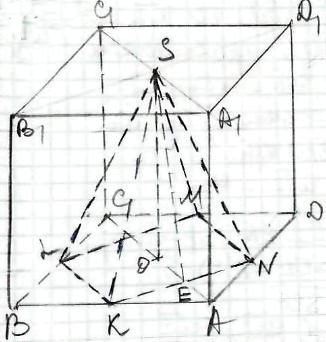
АВСDА1В1С1D1 - куб,
т.S = А1С1 ∩ В1D1,
К, L, М, N - середини ребер АВ, ВС, СD, АD відповідно.
SКLМN - піраміда.
КL - середня лінія ΔАВС, \begin{equation} KL=\frac{1}{2}AC \end{equation} МN - середня лінія ΔАВСD, \begin{equation} MN=\frac{1}{2}AC \end{equation} KL = MN,
KL║MN
LМ - середня лінія ΔBCD \begin{equation} LM=\frac{1}{2}BD \end{equation} КN - середня лінія ΔABD \begin{equation} KN=\frac{1}{2}BD, \end{equation} отже, LM = KN,
LM║KN.
Так як АС ┴ ВD,
то КL ┴ МL.
Тому KLМN - правильний чотирикутник, тобто квадрат.
SKLMN - правильна піраміда.
Так як ребро куба а, то \begin{equation} KL=\frac{1}{2}AC= \end{equation} \begin{equation} =\frac{1}{2}a\sqrt{2}=\frac{a\sqrt{2}}{2} \end{equation} Проведемо SЕ ┴ KN,
SЕ - апофема.
Із ΔSОЕ (∠SОЕ = 90°) \begin{equation} SE=\sqrt{OE^{2}+SO^{2}} \end{equation} \begin{equation} OE=\frac{1}{2}KL= \end{equation} \begin{equation} =\frac{1}{2}\cdot \frac{a\sqrt{2}}{2}=\frac{a\sqrt{4}}{2} \end{equation} SО = АА1 - а, тоді \begin{equation} SE= \end{equation} \begin{equation} =\sqrt{(\frac{a\sqrt{2}}{4})^{2}+a^{2}}= \end{equation} \begin{equation} =\frac{3a}{2\sqrt{2}} \end{equation} Площа бічної поверхні піраміди SКLМN: \begin{equation} S_{біч.}=\frac{1}{2}\cdot P_{KLMN}\cdot SE= \end{equation} \begin{equation} =\frac{1}{2}\cdot 4\frac{a\sqrt{3}}{2}\cdot \frac{3a}{2\sqrt{2}}= \end{equation} \begin{equation} =\frac{3a^{2}}{2}. \end{equation} \begin{equation} Відповідь: \frac{3a^{2}}{2} \end{equation}