вправа 4.3 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 4.3
Умова:
За стороною основи а і бічним ребром b знайдіть висоту правильної піраміди:
1) трикутної;
2) чотирикутної;
3) шестикутної.
1) трикутної;
2) чотирикутної;
3) шестикутної.
Розв'язання:
1) 
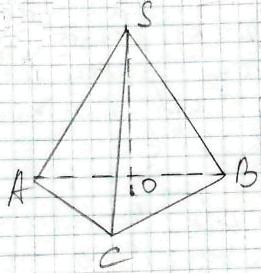SАВС - правильна піраміда.
ΔАВС - рівносторонній,
SА = SВ = SС = b,
SО - висота піраміди,
т.О - центр, ΔАВС - центр кола описаного навколо ΔАВС,
ОА - радіус кола \begin{equation} AO=\frac{a}{\sqrt{3}}. \end{equation} Із ΔАОS (∠АОS = 90°) \begin{equation} SA=\sqrt{AO^{2}+SO^{2}}, \end{equation} звідки \begin{equation} SO=\sqrt{SA^{2}-OA^{2}}= \end{equation} \begin{equation} =\sqrt{b^{2}-(\frac{a}{\sqrt{3}})^{2}}= \end{equation} \begin{equation} =\sqrt{b^{2}-\frac{a^{2}}{\sqrt{3}}}. \end{equation}
2)
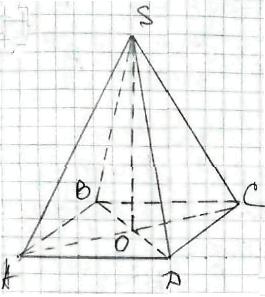SАВСD - правильна піраміда.
АВСD - квадрат,
АВ = а SО - висота,
т.О - точка перетину АС і ВD.
Бічні ребра SА = SВ = SС = SD. \begin{equation} SO=\sqrt{SA^{2}-OA^{2}} \end{equation} \begin{equation} OA=\frac{1}{2}AC= \end{equation} \begin{equation} =\frac{1}{2}\cdot a\sqrt{2}=\frac{a\sqrt{2}}{2} \end{equation} \begin{equation} SO= \end{equation} \begin{equation} =\sqrt{b^{2}-(\frac{a\sqrt{2}}{2})^{2}}= \end{equation} \begin{equation} =\sqrt{b^{2}-\frac{a^{2}}{2}}. \end{equation}
3)
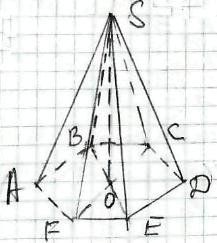SАВСDЕF - правильна піраміда,
АВ = а, SА = b,
SО - висота,
т.О - точка перетину АD, ВЕ і FС. \begin{equation} AO=\frac{1}{2}AD= \end{equation} \begin{equation} =\frac{1}{2}2\cdot AB=AB=a \end{equation} Із ΔSАО (∠SОА = 90°) \begin{equation} SO=\sqrt{SA^{2}-AO^{2}}= \end{equation} \begin{equation} =\sqrt{b^{2}-a^{2}}. \end{equation} Відповідь: \begin{equation} 1)\sqrt{b^{2}-\frac{a^{2}}{\sqrt{3}}}; \end{equation} \begin{equation} 2)\sqrt{b^{2}-\frac{a^{2}}{2}}; \end{equation} \begin{equation} 3)\sqrt{b^{2}-a^{2}} \end{equation}
SАВС - правильна піраміда. ΔАВС - рівносторонній,
SА = SВ = SС = b,
SО - висота піраміди,
т.О - центр, ΔАВС - центр кола описаного навколо ΔАВС,
ОА - радіус кола \begin{equation} AO=\frac{a}{\sqrt{3}}. \end{equation} Із ΔАОS (∠АОS = 90°) \begin{equation} SA=\sqrt{AO^{2}+SO^{2}}, \end{equation} звідки \begin{equation} SO=\sqrt{SA^{2}-OA^{2}}= \end{equation} \begin{equation} =\sqrt{b^{2}-(\frac{a}{\sqrt{3}})^{2}}= \end{equation} \begin{equation} =\sqrt{b^{2}-\frac{a^{2}}{\sqrt{3}}}. \end{equation}
2)
SАВСD - правильна піраміда. АВСD - квадрат,
АВ = а SО - висота,
т.О - точка перетину АС і ВD.
Бічні ребра SА = SВ = SС = SD. \begin{equation} SO=\sqrt{SA^{2}-OA^{2}} \end{equation} \begin{equation} OA=\frac{1}{2}AC= \end{equation} \begin{equation} =\frac{1}{2}\cdot a\sqrt{2}=\frac{a\sqrt{2}}{2} \end{equation} \begin{equation} SO= \end{equation} \begin{equation} =\sqrt{b^{2}-(\frac{a\sqrt{2}}{2})^{2}}= \end{equation} \begin{equation} =\sqrt{b^{2}-\frac{a^{2}}{2}}. \end{equation}
3)
SАВСDЕF - правильна піраміда, АВ = а, SА = b,
SО - висота,
т.О - точка перетину АD, ВЕ і FС. \begin{equation} AO=\frac{1}{2}AD= \end{equation} \begin{equation} =\frac{1}{2}2\cdot AB=AB=a \end{equation} Із ΔSАО (∠SОА = 90°) \begin{equation} SO=\sqrt{SA^{2}-AO^{2}}= \end{equation} \begin{equation} =\sqrt{b^{2}-a^{2}}. \end{equation} Відповідь: \begin{equation} 1)\sqrt{b^{2}-\frac{a^{2}}{\sqrt{3}}}; \end{equation} \begin{equation} 2)\sqrt{b^{2}-\frac{a^{2}}{2}}; \end{equation} \begin{equation} 3)\sqrt{b^{2}-a^{2}} \end{equation}
