вправа 4.6 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 4.6
Умова:
Знайдіть площу повної поверхні правильної шестикутної піраміди, якщо її бічне ребро дорівнює а і радіус кола, вписаного в основу, r.
Розв'язання:
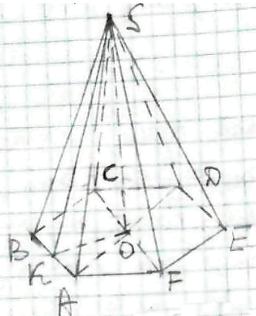
SАВСDЕF - правильна піраміда,
SО - висота піраміди,
т.О - точка перетину АD і СF (центр вписаного і описаного кіл).
SА = а.
Проведемо ОК ┴ АВ,
тоді ОК = r - радіус вписаного кола в основу.
Тоді \begin{equation} AB=\frac{2r}{\sqrt{3}}. \end{equation} Знайдемо АО - радіус кола, описаного навколо основи призми: \begin{equation} AO=AB=\frac{2r}{\sqrt{3}}. \end{equation} Із ΔSАО (∠SОА = 90°) \begin{equation} SO=\sqrt{SA^{2}-AO^{2}}= \end{equation} \begin{equation} =\sqrt{a^{2}-\frac{4r^{2}}{3}}. \end{equation} Проведемо SК.
За теоремою про три перпендикуляри так, як ОК ┴ АВ,
то SК ┴ АВ,
тоді SК - апофема піраміди.
Із ΔSОК (∠SОК = 90°) \begin{equation} SK=\sqrt{SO^{2}+OK^{2}}= \end{equation} \begin{equation} =\sqrt{a^{2}-\frac{4r^{2}}{3}+r^{2}}= \end{equation} \begin{equation} =\sqrt{a^{2}-\frac{r^{2}}{3}} \end{equation} Sповн. = Sбіч. + Sосн. = \begin{equation} =\frac{1}{2}P_{осн.}\cdot SK+S_{осн.}= \end{equation} \begin{equation} =\frac{1}{2}\cdot 6\cdot \end{equation} \begin{equation} \cdot \frac{2r}{\sqrt{3}}\cdot \sqrt{a^{2}-\frac{r^{2}}{3}}+ \end{equation} \begin{equation} +\frac{3\sqrt{3}}{2}\cdot \frac{4r^{2}}{3}= \end{equation} \begin{equation} =2r\sqrt{3}\frac{1}{\sqrt{3}}\sqrt{3a^{2}-r^{2}}+ \end{equation} \begin{equation} +2\sqrt{3}r^{2}= \end{equation} \begin{equation} =2r(\sqrt{3a^{2}-r^{2}}+\sqrt{3}r). \end{equation} Відповідь: \begin{equation} 2r(\sqrt{3a^{2}-r^{2}}+\sqrt{3}r) \end{equation}