вправа 5.1 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 5.1
Умова:
Основа піраміди – прямокутник зі сторонами 6 см і 8 см. Кожне бічне ребро піраміди дорівнює 13 см. Знайдіть висоту піраміди.
Розв'язання:
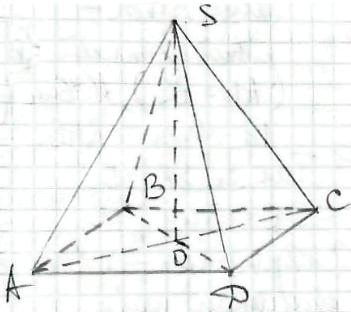Нехай SАВСD - піраміда,
АВСD - прямокутник,
АА = 6 см,
ВС = 8 см.
Оскільки за умовою
SА = SВ = SС = SD = 13 см,
то основою висоти SО піраміди є центр кола, описаного навколо АВСD.
Тоді т.О - основа висоти є точкою перетину АС і BD.
Із ΔАВС (∠АВС = 90°) \begin{equation} AC=\sqrt{AB^{2}+BC^{2}}= \end{equation} \begin{equation} =\sqrt{6^{2}+8^{2}}=10 (см) \end{equation} \begin{equation} AO=\frac{1}{2}AC= \end{equation} \begin{equation} =\frac{1}{2}\cdot 10=5 (см) \end{equation} Із ΔSAO (∠SОА = 90°) \begin{equation} SO=\sqrt{SA^{2}-AO^{2}}= \end{equation} \begin{equation} =\sqrt{13^{2}-5^{2}}=12 (см). \end{equation} Відповідь: 12 см
Нехай SАВСD - піраміда, АВСD - прямокутник,
АА = 6 см,
ВС = 8 см.
Оскільки за умовою
SА = SВ = SС = SD = 13 см,
то основою висоти SО піраміди є центр кола, описаного навколо АВСD.
Тоді т.О - основа висоти є точкою перетину АС і BD.
Із ΔАВС (∠АВС = 90°) \begin{equation} AC=\sqrt{AB^{2}+BC^{2}}= \end{equation} \begin{equation} =\sqrt{6^{2}+8^{2}}=10 (см) \end{equation} \begin{equation} AO=\frac{1}{2}AC= \end{equation} \begin{equation} =\frac{1}{2}\cdot 10=5 (см) \end{equation} Із ΔSAO (∠SОА = 90°) \begin{equation} SO=\sqrt{SA^{2}-AO^{2}}= \end{equation} \begin{equation} =\sqrt{13^{2}-5^{2}}=12 (см). \end{equation} Відповідь: 12 см
