вправа 5.10 гдз 11 клас математика (геометрія) Нелін Долгова 2019

11 клас ➠ математика ➠ Нелін Долгова

 

Вправа 5.10


Умова: 

 

В основі піраміди MABCD лежить ромб ABCD із діагоналями АС = 6, BD = 8, а всі бічні грані утворюють з основою кути по 45°. Знайдіть:
1) висоту піраміди;
2) відстань від вершини М до ребра основи.

 

Розв'язання:



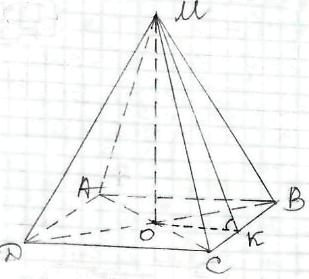МАВСD - піраміда,
АВСD - ромб,
АС = 6,
ВD - 8,
МО - висота піраміди.
Так як усі бічні грані піраміди утворюють однакові кути її основою, то т.О - центр кола, вписаного в основу АВСD.
Нехай ОК - радіус цього кола,
тоді ∠МКО = 45°.
Так як МО ┴ АВСD,
то ∠МОК = 90°.
Так як ОК ┴ ВС,
то за теоремою про три перпендикуляри
ВС ┴ МК.
1) АВСD - ромб,
тоді АС ┴ ВD,
отже ΔВОК - прямокутний, \begin{equation} OK=\frac{OC\cdot OB}{BC} \end{equation} \begin{equation} OC=\frac{1}{2}AC= \end{equation} \begin{equation} =\frac{1}{2}\cdot 6=3 \end{equation} \begin{equation} OB=\frac{1}{2}BD= \end{equation} \begin{equation} =\frac{1}{2}\cdot 8=4 \end{equation} \begin{equation} BC=\sqrt{OC^{2}+OB^{2}}= \end{equation} \begin{equation} =\sqrt{3^{2}+4^{2}}=5 \end{equation} \begin{equation} OK=\frac{3\cdot 4}{5}=2,4 \end{equation} Із ΔМОК (∠МОК = 90°)
МО = ОК = 2,4 так як ΔМОК - рівнобедрений. \begin{equation} 2)MK=\sqrt{MO^{2}+OK^{2}}= \end{equation} \begin{equation} =\sqrt{(\frac{12}{5})^{2}\cdot 2}= \end{equation} \begin{equation} =\frac{12\sqrt{2}}{5}. \end{equation} \begin{equation} Відповідь: 1) 2,4; \frac{12\sqrt{2}}{5} \end{equation}