вправа 5.12 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 5.12
Умова:
Основа піраміди – прямокутний трикутник із катетами 6 см і 8 см. Усі двогранні кути при основі піраміди дорівнюють 60°. Знайдіть висоту піраміди.
Розв'язання:
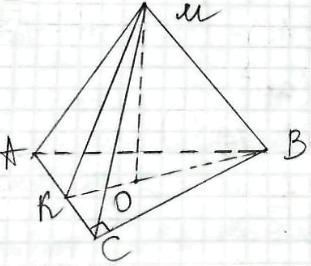МАВС - піраміда,
∠АСВ = 90°,
АС = 6 см,
ВС = 8 см,
МО - висота піраміди.
Так як усі двогранні кути при основі піраміди рівні,
то т.О - центр кола, вписаного в ΔАВС.
Нехай ОК - радіус цього кола.
Так як АС ┴ ОК,
то за теоремою про три перпендикуляри
АС ┴н МК,
тоді ∠МКО - лінійний кут двогранного кута,
∠МКО = 60°.
Із ΔАВС (∠АСВ = 90°): \begin{equation} AB=\sqrt{AC^{2}+BC^{2}}= \end{equation} \begin{equation} =\sqrt{6^{2}+8^{2}}=10 \end{equation} \begin{equation} OK=\frac{S_{\Delta ABC}}{p}, \end{equation} де SΔАВС і р - площа і півпериметр ΔАВС \begin{equation} S_{\Delta ABC}= \end{equation} \begin{equation} =\frac{1}{2}AC\cdot BC= \end{equation} \begin{equation} =\frac{1}{2}6\cdot 8=24 (см^{2}) \end{equation} \begin{equation} p=\frac{1}{2}(AB+BC+AC)= \end{equation} \begin{equation} =\frac{1}{2}(10+8+6)=12 (см) \end{equation} \begin{equation} OK=\frac{24}{12}=2 (см) \end{equation} Із ΔМОК (∠МОК = 90°)
МО = ОКtg∠МКО =
= 2tg60° = 2√3 (см).
Відповідь: 2√3 см