вправа 5.13 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 5.13
Умова:
Основа піраміди – рівнобедрений трикутник зі сторонами 40 см, 25 см і 25 см. Висота піраміди завдовжки 8 см проходить через вершину кута основи, протилежного стороні завдовжки 40 см. Знайдіть площу бічної поверхні піраміди.
Розв'язання:
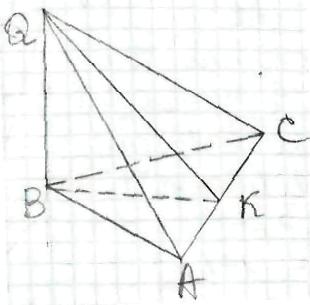QАВСК - піраміда,
АВ = ВС = 25 см,
АС = 40 см,
QВ - висота піраміди,
QВ = 8 см.
Знайдемо Sбіч. - площу бічної поверхні
Sбіч. = SΔАВQ + SΔСВQ + SΔАСQ.
Так як QВ висота піраміди,
то QВ ┴ (АВС),
тоді QВ ┴ АВ і
QВ ┴ СВ.
Із ΔАВQ (∠АВQ = 90°) \begin{equation} S_{\Delta ABQ}=\frac{1}{2}AB\cdot BQ= \end{equation} \begin{equation} =\frac{1}{2}25\cdot 8=100 (см^{2}) \end{equation} Так як ΔСВQ = ΔАВQ
(АВ = ВС,
QВ - спільний катет),
то SΔСВQ = 100 см2.
Проведемо QК ┴ АС,
за теоремою про три перпендикуляри А
С ┴ ВК,
отже QК - висота ΔАВС.
Тоді \begin{equation} BK=\sqrt{AB^{2}-AK^{2}} \end{equation} ΔАВС - рівнобедрений, тому \begin{equation} AK=\frac{1}{2}AC= \end{equation} \begin{equation} =\frac{1}{2}\cdot 40=20 (см) \end{equation} \begin{equation} BK=\sqrt{25^{2}-20^{2}}= \end{equation} \begin{equation} =15 (см) \end{equation} Із ΔQВК (∠QВК = 90°) \begin{equation} QK=\sqrt{QB^{2}+BK^{2}} \end{equation} \begin{equation} QK=\sqrt{8^{2}+15^{2}}=17 (см) \end{equation} \begin{equation} S_{\Delta ACQ}=\frac{1}{2}AC\cdot QK \end{equation} \begin{equation} =\frac{1}{2}40\cdot 17=340 (см^{2}) \end{equation} Sбіч. = 100 + 100 +
+ 340 = 540 (см2).
Відповідь: 540 см2