вправа 5.3 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 5.3
Умова:
В основі піраміди лежить прямокутний трикутник із гіпотенузою с. Кожне бічне ребро утворює з площиною основи кут β. Знайдіть висоту піраміди.
Розв'язання:
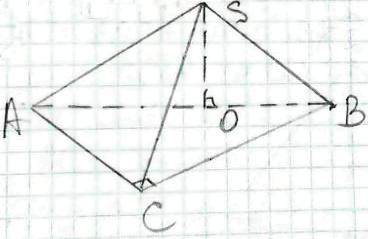SАВС - піраміда,
ΔАВС - прямокутний (∠АСВ = 90°),
АВ = С.
Оскільки всі бічні ребра нахилені під різними кутами до площини основи, то основою висоти SО піраміди є центр кола, описаного навколо основи піраміди,
тобто т.О - середина АВ.
Оскільки АО - проекція ребра SА на площину АВС,
то ∠SАО - кут між ребром SА і площиною основи
(за умовою ∠SАО = β).
Знайдемо SО. \begin{equation} AO=\frac{1}{2}AB=\frac{C}{2} \end{equation} Із ΔSАО (∠SОА = 90°) \begin{equation} SO=AO\cdot tg\beta = \end{equation} \begin{equation} =\frac{C}{2}tg\beta . \end{equation} \begin{equation} Відповідь: \frac{C}{2}tg\beta \end{equation}
SАВС - піраміда, ΔАВС - прямокутний (∠АСВ = 90°),
АВ = С.
Оскільки всі бічні ребра нахилені під різними кутами до площини основи, то основою висоти SО піраміди є центр кола, описаного навколо основи піраміди,
тобто т.О - середина АВ.
Оскільки АО - проекція ребра SА на площину АВС,
то ∠SАО - кут між ребром SА і площиною основи
(за умовою ∠SАО = β).
Знайдемо SО. \begin{equation} AO=\frac{1}{2}AB=\frac{C}{2} \end{equation} Із ΔSАО (∠SОА = 90°) \begin{equation} SO=AO\cdot tg\beta = \end{equation} \begin{equation} =\frac{C}{2}tg\beta . \end{equation} \begin{equation} Відповідь: \frac{C}{2}tg\beta \end{equation}
