вправа 5.4 гдз 11 клас математика (геометрія) Нелін Долгова 2019

11 клас ➠ математика ➠ Нелін Долгова

 

Вправа 5.4


Умова: 

 

Основа піраміди – рівнобедрений трикутник із бічною стороною а і кутом при основі α. Усі бічні ребра піраміди утворюють з її висотою кут φ. Знайдіть висоту піраміди.

 

Розв'язання:



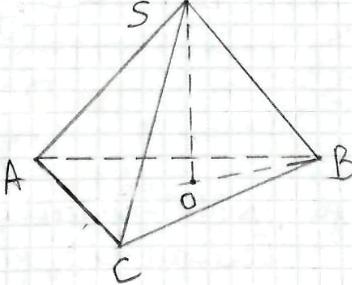SАВС - піраміда,
АВ = ВС = а,
∠ВАС = α.
Нехай SО - висота піраміди.
Оскільки всі бічні ребра піраміди утворюють рівні кути з висотою піраміди, то т.О - центр кола, описаного навколо ΔАВС.
За умовою ∠ВSО = φ.
Знайдемо SО.
Із ΔАВС:
∠АВС = 180° - 2α.
За теоремою косинусів:
АС2 = АС² + ВС² -
- 2АВ • ВСcos∠АВС
АС2 = а² + а² -
- 2а²cos(180° - 2α)
АС² = 2а² + 2а²cos2α
АС² = 2а²(1 + cos2α)
АС² = 2а² • 2cos²α
АС = 2аcosα
Площа ΔАВС: \begin{equation} S_{\Delta ABC}=\frac{1}{2}AB\cdot \end{equation} \begin{equation} \cdot BCsin\angle ABC \end{equation} \begin{equation} S_{\Delta ABC}= \end{equation} \begin{equation} =\frac{1}{2}a^{2}sin(180^{\circ}-2\alpha ) \end{equation} \begin{equation} S_{\Delta ABC}=\frac{1}{2}a^{2}sin2\alpha \end{equation} Так як ОВ - радіус кола, описаного навколо ΔАВС, то \begin{equation} OB=\frac{a\cdot a\cdot 2acos\alpha }{4\cdot \frac{1}{2}a^{2}sin2\alpha } \end{equation} \begin{equation} OB=\frac{a\cdot cos\alpha }{sin2\alpha } \end{equation} \begin{equation} OB=\frac{a}{2sin\alpha } \end{equation} Із ΔSОВ (∠SОВ = 90° \begin{equation} SO=\frac{OB}{tg\angle BSO} \end{equation} \begin{equation} SO=\frac{a}{2sin\alpha tg\varphi }= \end{equation} \begin{equation} =\frac{actg\varphi }{2sin\alpha }. \end{equation} \begin{equation} Відповідь: \frac{actg\varphi }{2sin\alpha } \end{equation}