вправа 5.6 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 5.6
Умова:
Основа піраміди – трикутник зі сторонами 13 см, 14 см і 15 см. Бічне ребро, протилежне середній за довжиною стороні основи, перпендикулярне до площини основи й дорівнює 16 см. Знайдіть площу повної поверхні піраміди.
Розв'язання:
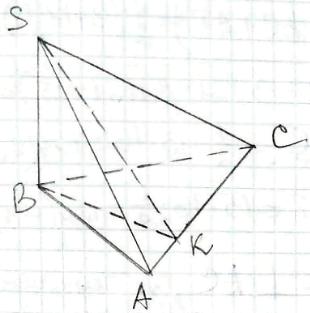SАВС - піраміда,
АВ = 13 см,
ВС = 15 см,
АС = 14 см,
SВ ┴ (АВС),
тоді SВ = 16 см - висота піраміди і
SВ ┴ АВ,
SВ ┴ ВС.
Знайдемо Sпов. - площу повної поверхні піраміди.
Sпов. = SΔАВС + SΔАВS +
+ SΔСВS + SΔАСS,
де SΔАВС - площа ΔАВС,
SΔСВS - площа ΔСВS,
SΔАВS - площа ΔАВS,
SΔАСS - площа ΔАСS. \begin{equation} S_{\Delta ABC}=\sqrt{p(p-AB)} \end{equation} \begin{equation} \sqrt{(p-BC)(p-AC)}, \end{equation} \begin{equation} p=\frac{1}{2}(AB+BC+AC)= \end{equation} \begin{equation} =\frac{1}{2}(13+14+15)= \end{equation} \begin{equation} =21 (см) \end{equation} \begin{equation} S_{\Delta ABC}=\sqrt{21(21-13)} \end{equation} \begin{equation} \sqrt{(21-14)(21-15)}= \end{equation} \begin{equation} =84 (см^{2}) \end{equation} \begin{equation} S_{\Delta ABS}=\frac{1}{2}AB\cdot BS= \end{equation} \begin{equation} =\frac{1}{2}\cdot 13\cdot 16=104 (см^{2}) \end{equation} \begin{equation} S_{\Delta CBS}=\frac{1}{2}BC\cdot BS= \end{equation} \begin{equation} =\frac{1}{2}\cdot 15\cdot 16=120 (см^{2}) \end{equation} Проведемо ВК ┴ АС, за теоремою про три перпендикуляри
SК ┴ АС,
тоді ∠ВКS - кут між(АВС) і (АSС).
Так як ΔАВС - ортогональна проекція ΔАSС, то \begin{equation} S_{\Delta ACS}=\frac{S_{\Delta ABC}}{cos\angle BKS} \end{equation} Із ΔАВС знайдемо ВК: \begin{equation} S_{\Delta ABC}=\frac{1}{2}BK\cdot AC, \end{equation} звідки \begin{equation} BK=\frac{2S_{\Delta ABC}}{AC} \end{equation} \begin{equation} BK=\frac{2\cdot 84}{14}=12 (см) \end{equation} \begin{equation} cos\angle BKS=\frac{BK}{SK} \end{equation} \begin{equation} SK=\sqrt{BK^{2}+BS^{2}}= \end{equation} \begin{equation} =\sqrt{12^{2}+16^{2}}=20 (см) \end{equation} \begin{equation} S_{\Delta ACS}=\frac{84\cdot 20}{12}= \end{equation} \begin{equation} =140 (см^{2}) \end{equation} Sпов. = 84 + 104 + 120 +
+ 140 = 448 (см2).
Відповідь: 448 см2