вправа 6.5 гдз 11 клас математика (геометрія) Нелін Долгова 2019

Вправа 6.5


Умова: 

Розв'язання:

1)

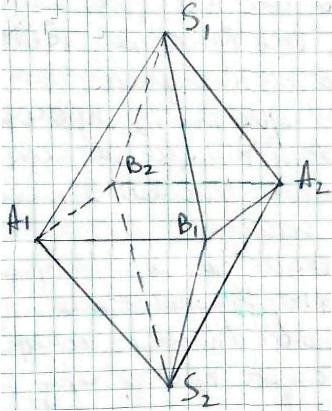В оксаедрі через пару вершин S₁ і S₂ проходять чотири площини симетрії (дві через ребра А₁S₁ і А₂S₂ і В₁S₁ та В₂S₂. Також дві площини проходять через вісь S₁S₂ перпендикулярно ребром А₁В₁ та А₂В₂, а також ребром В₁А₂ та А₂В₂. Аналогічно через А₁ і А₂ проходять 4 площини, але площина через А₁S₁ та А₂S₁ вже врахована. Тобто отримуємо 3 площини.
Крім того, через В₁ і В₂ проходять 2 невраховані раніше площини.
Отже, маємо загалом 9 площин симетрії октаедра.
2) Площини симетрії правильного додекаедра проходять через ребро, яке містить вершину перпендикулярно протилежному ребру. Тому через першу пару протилежних п'ятикутників проходить 5 площин, через другу пару - 4, через третю - 3, через четверту - 2, через п'яту - 1.
Отже, правильний додекаедр має 15 площин симетрії.
3) В правильному ікосаедрі 12 вершин. Через першу пару протилежних вершин проходе 5 площин симетрії (кожна площина проходе через ребро, яке містить вершину, перпендикулярно протилежному куту).
Через другу пару протилежних вершин також проходять 5 площин, з яких одна вже врахована, отже маємо 4 нові площини симетрії. Для третьої пари маємо 3 нові площини, для четвертої - 2, для п'ятої - одну нову площини.
Отже, ікосаедр має 15 площин симетрії
(5 + 4 + 3 + 2 + 1 = 15).
Відповідь: 1) 9; 2) 15; 3) 15