вправа 7.13 гдз 11 клас математика (геометрія) Нелін Долгова 2019

Вправа 7.13


Умова: 

Діагональ розгортки бічної поверхні циліндра дорівнює d і утворює кут φ з основою розгортки. Знайдіть площу повної поверхні циліндра.

Розв'язання:


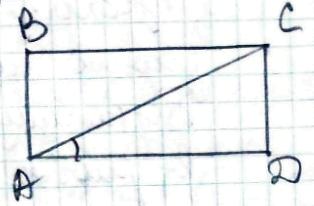
Нехай прямокутник ABCD є розгорнутою циліндра,
АС = d, ∠САD = φ.
Знайдемо S_пов. - площу повної поверхні циліндра.
Із ΔАСD (∠АDС = 90°)
АD = АСcos∠САD = dcosφ
СD = АСsin∠САD = dsinφ
Так як АD = 2πR - довжина кола основи циліндра, то \begin{equation} R=\frac{AD}{2\Pi }=\frac{dcos\varphi }{2\Pi } \end{equation} Так як S_пов. = 2πR(R + 4), то \begin{equation} S_{пов.}=2\Pi \cdot \frac{dcos\varphi }{2\Pi } \end{equation} \begin{equation} (\frac{dcos\varphi }{2\Pi }+dsin\varphi )= \end{equation} \begin{equation} =dcos\varphi (\frac{dcos\varphi }{2\Pi }+dsin\varphi )= \end{equation} \begin{equation} =\frac{d^{2}cos^{2}\varphi }{2\Pi }+d^{2}cos\varphi sin\varphi . \end{equation} Відповідь: \begin{equation} S_{пов.}=2\Pi \cdot \frac{dcos\varphi }{2\Pi } \end{equation} \begin{equation} (\frac{dcos\varphi }{2\Pi }+dsin\varphi )= \end{equation} \begin{equation} =dcos\varphi (\frac{dcos\varphi }{2\Pi }+dsin\varphi )= \end{equation} \begin{equation} \frac{d^{2}cos^{2}\varphi }{2\Pi }+d^{2}cos\varphi sin\varphi \end{equation}