вправа 7.7 гдз 11 клас математика (геометрія) Нелін Долгова 2019

Вправа 7.7


Умова: 

Діагональ осьового перерізу циліндра дорівнює 48 см, а кут між цією діагоналлю й віссю циліндра становить 60°. Знайдіть:
1) висоту циліндра;
2) радіус основи циліндра;
3) площу основи циліндра.

Розв'язання:


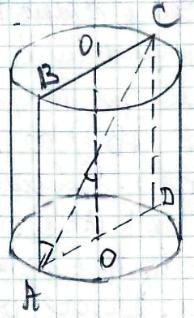
Нехай АВСD - осьовий переріз,
АС = 48 см - діагональ перерізу.
ОО₁ - вісь циліндра.
Так як АВ║ОО₁, то кут між АС і ОО₁ дорівнює куту між АС і АВ,
тоді ∠ВАС = 60°.
Із ΔАВС (∠АВС = 90°)
АВ = АСcos∠ВАС =
= 48cos60° = 24 (см) - висота циліндра.
ВС = АСsin∠ВАС = 48sin60° = \begin{equation} =\frac{48\sqrt{3}}{2}=24\sqrt{3} (см) \end{equation} \begin{equation} BO_{1}=\frac{1}{2}BC= \end{equation} \begin{equation} =\frac{1}{2}\cdot 24\sqrt{3}=12\sqrt{3} (см) \end{equation} R = ВО₁ = 12√3 (см) - радіус циліндра
S_осн. = πR² - площа основи
S_осн. = π(12√3)² = 432π (см²).
Відповідь: 1) 24 см; 2) 12√3 см; 3) 432π см²