вправа 7.8 гдз 11 клас математика (геометрія) Нелін Долгова 2019

Вправа 7.8


Умова: 

У циліндрі паралельно його осі проведено площину, що відтинає від кола основи дугу 120°. Довжина відрізка осі між центрами основ становить 10 см, відстань від осі до січної площини дорівнює 2 см. Знайдіть площу перерізу.

Розв'язання:


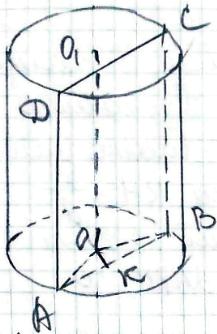
Нехай ОО₁ - ось циліндра.
ABCD - площина ОО₁║(АВСD).
Так як АD║ОО₁, ОО₁ ┴ (АВО),
то АD ┴ (АВО) і (АВСD) ┴ АВО.
Проведемо ОК ┴ АВ,
тоді ОК ┴ (АВСD),
ОК - відстань від осі до січної площини.
За умовою ОК = 2 см,
∠АОВ = 120° - кут,
що перетинає (АВСD) від кола основи,
ОО₁ = 10 см.
Знайдемо S_АВСD - площу перерізу АВСD.
Так, як ΔАВСD - рівнобедрений,
ОК ┴ АВ, то ОК - медіана ΔАВО і його бісектриса.
Тоді \begin{equation} \angle AOK=\frac{1}{2}\angle AOB= \end{equation} \begin{equation} =\frac{1}{2}\cdot 120^{\circ}=60^{\circ} \end{equation} Із ΔАОК (∠АКО = 90°)
АК = ОКtg∠АОК =
= 2tg60° = 2√3 (см).
Тоді АВ = 2 • АК = 4√3 (см)
АD = ОО₁ = 10 см
S_АВСD = АВ • АD =
= 4√3 • 10 = 40√3 (см²).
Відповідь: 40√3 см²