вправа 9.4 гдз 11 клас математика (геометрія) Нелін Долгова 2019

Вправа 9.4


Умова: 

Усі вершини квадрата зі стороною 8 дм належать сфері радіуса 9 дм. На якій відстані від центра сфери розташована площина квадрата?

Розв'язання:



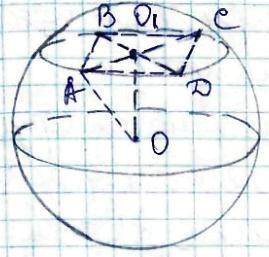Нехай задано сферу. 
т. О - центр,
ОА - радіус,
ОА = 9 дм.
Проведемо площину α, яка перетне сферу по колу, т. О₁ - центр цього кола, квадрат АВСD лежить в площині α і точки А, В, С, D належать сфері.
Тоді АВСD вписаний в коло,
тому ОО₁ - відстань від центра сфери до площини квадрата.
АС - діагональ АВСD,
тоді АС = АD√2 = 8√2 (дм) \begin{equation} O_{1}A=\frac{1}{2}AC= \end{equation} \begin{equation} =\frac{1}{2}\cdot 8\sqrt{2}=4\sqrt{2} (дм) \end{equation} Із ΔАО₁О (∠АО₁О = 90°) \begin{equation} OO_{1}=\sqrt{AO^{2}-AO_{1}^{2}}= \end{equation} \begin{equation} =\sqrt{9^{2}-(4\sqrt{2})^{2}}= \end{equation} \begin{equation} =\sqrt{81-32}=7 (дм) \end{equation} Відповідь: 7 дм