вправа 9.7 гдз 11 клас математика (геометрія) Нелін Долгова 2019

Вправа 9.7


Умова: 

Сфера проходить через усі вершини прямокутного трикутника з катетами 6 і 8, а центр сфери віддалений від площини цього трикутника на відстань 12. Знайдіть радіус сфери.

Розв'язання:



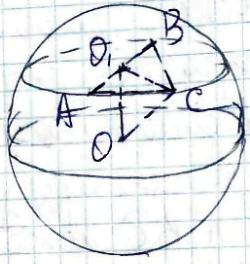Нехай задано сфера, т. О - центр сфери.
Проведемо площину α, яка перетинає сферу по колу, т. А, В, С лежать на сфері,
тому ΔАВС - вписаний в це коло.
Нехай О₁ - центр цього кола.
Так як ΔАВС - прямокутний
(∠АСВ = 90°),
то т. О - середина АВ,
О₁С - радіус кола від т. О до площини ΔАВС.
Знайдемо ОС - радіус сфери.
Із ΔАВС (∠АСВ = 90°) \begin{equation} AB=\sqrt{AC^{2}+BC^{2}}= \end{equation} \begin{equation} =\sqrt{6^{2}+8^{2}}=10 \end{equation} \begin{equation} AO_{1}=\frac{1}{2}\cdot AB= \end{equation} \begin{equation} =\frac{1}{2}\cdot 10=5 \end{equation} АО₁ = О₁С = 5.
Із ΔОО1С (∠ОО1С = 90°) \begin{equation} OC=\sqrt{OO_{1}^{2}+O_{1}C^{2}}= \end{equation} \begin{equation} =\sqrt{12^{2}+5^{2}}=13. \end{equation} Відповідь: 13