вправа 2.3.1 гдз 11 клас математика Нелін Долгова 2019

Відповідь ГДЗ:

1) 2^x > 1
2^x > 2⁰
x > 0, так як a = 2 > 1.
Відповідь: (0; +∞) \begin{equation} 2)2^{x}=\frac{1}{3} \end{equation} 2^x > 2^-1
Так, як а = 2 > 1, то
х > -1.
Відповідь: (-1; +∞)
3) 3^х > 0
х ∈ (-∞; +∞).
Відповідь: (-∞; +∞) \begin{equation} 4)(\frac{1}{3})^{x}<0 \end{equation} Немає розв'язків, так як область
значень функції а^х (0; +∞).
Відповідь: немає розв'язків \begin{equation} 5)(\frac{1}{3})^{x}\geq 9 \end{equation} \begin{equation} (\frac{1}{3})^{x}\geq 3^{2} \end{equation} \begin{equation} (\frac{1}{3})^{x}\geq (\frac{1}{3})^{-2} \end{equation} Так, як \begin{equation} y=(\frac{1}{3})^{x} \end{equation} спадна функція, то х < -2.
Відповідь: (-∞; -2] \begin{equation} 6)(\frac{1}{2})^{3-x}\leq 4 \end{equation} \begin{equation} (\frac{1}{2})^{3-x}\leq 2^{2} \end{equation} \begin{equation} (\frac{1}{2})^{3-x}\leq (\frac{1}{2})^{-2} \end{equation} Так, як \begin{equation} (\frac{1}{2})^{x} \end{equation} спадна, то
3 - х ≥ -2
-x ≥ -5 | : (-1)
x ≤ 5.
Відповідь: (-∞; 5]
7) 5^х ≥ 25√5
5^х ≥ 5² • 5^0,5
5^х ≥ 5^2,5
Так, як у = 5х зростаюча функція, то
х ≥ 2,5.
Відповідь: [2,5; +∞) \begin{equation} 8)(\frac{1}{4})^{x-2}<16 \end{equation} \begin{equation} (\frac{1}{4})^{x-2}<4^{2} \end{equation} \begin{equation} (\frac{1}{4})^{x-2}<(\frac{1}{4})^{-2} \end{equation} Так, як \begin{equation} y=(\frac{1}{4})^{x} \end{equation} спадна функція, то
х - 2 > -2
x > 0.
Відповідь: (0; +∞) \begin{equation} 9)0,3^{\frac{x^{2}-7x+6}{x-3}}\leq 1 \end{equation} Так, як у = 0,3х спадна функція, то \begin{equation} \frac{x^{2}-7x+6}{x-3}\geq 0 \end{equation} Розв'яжемо методом інтервалів.
Нулі чисельника:
х² - 7х + 6 = 0
х₁ = 6, х₂ = 1
Нулі знаменника:
х - 3 = 0
х = 3


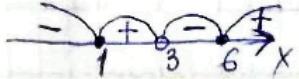
х ∈ [1; 3) U [6; +∞).
Відповідь: [1; 3) U [6; +∞) \begin{equation} 10)1,3^{\frac{x^{2}-9x+8}{x-4}}\leq 1 \end{equation} Так, як у = 1,3х зростаюча
функція, то \begin{equation} \frac{x^{2}-9x+8}{x-4}\geq 0 \end{equation} Нулі чисельника:
х² - 9х + 8 = 0
х₁ = 1, х₂ = 8
Нулі знаменника:
х - 4 = 0
х = 4


х ∈ [1; 4) U [8; +∞).
Відповідь: [1; 4) U [8; +∞)