вправа 4.1.1 гдз 11 клас математика Нелін Долгова 2019
Вправа 4.1.1
Умова:
Умова:
Знайдіть область визначення функції:
Відповідь ГДЗ:
1) y = log11(2x + 6)
2x + 6 > 0
2x > -6 x > -3
Д(у) = (-3; +∞).
Відповідь: (-3; +∞) \begin{equation} 2)y=log_{\frac{1}{6}}(x-3) \end{equation} x - 3 > 0
x > 3
Д(у) = (3; +∞).
Відповідь: (3; +∞) \begin{equation} 3)y=log_{\sqrt{2}}(x^{2}-1) \end{equation} x2 - 1 > 0
x2 - 1 = 0
x2 = 1
x1 = -1, x2 = 1
Д(у) = (-∞; -1) U (1; +∞).
Відповідь: (-∞; -1) U (1; +∞)
4) у = log5,2(3x - x2)
3x - x2 > 0
x2 - 3x < 0
x2 - 3x = 0
x(x - 3) = 0
x1 = 0, x2 = 3

Д(у) = (0; 3).
Відповідь: (0; 3) \begin{equation} 5)y=log_{\frac{3}{8}}(2x^{2}+1) \end{equation} 2x2 + 1 > 0
Нерівність виконується при будь-якому
значення х, отже Д(у) = (-∞; +∞).
Відповідь: R
6) y = logπ(х2 + х + 1)
х2 + х + 1 > 0
Д = 1 - 4 = -3 < 0
Нерівність виконується при будь-якому
значення х, тому Д(у) = (-∞; +∞).
Відповідь: R \begin{equation} 7)y=log_{0,4}\frac{2x-6}{x+2} \end{equation} \begin{equation} \frac{2x-6}{x+2}>0 \end{equation} \begin{equation} \frac{2x-6}{x+2}=0 \end{equation}Нулі чисельника:
2х - 6 = 0
х = 3
Нулі знаменника:
х + 2 = 0
х = -2

Д(у) = (-∞; -2) U (3; +∞).
Відповідь: (-∞; -2) U (3; +ЗБ) \begin{equation} 8)log_{\sqrt{7}}\frac{x^{2}-5x+6}{x-3} \end{equation} \begin{equation} \frac{x^{2}-5x+6}{x-3}>0 \end{equation} \begin{equation} \frac{x^{2}-5x+6}{x-3}=0 \end{equation} Нулі чисельника:
х2 - 5х + 6 = 0
х1 = 2, х2 = 3
Нулі знаменника:
х - 3 = 0
х = 3

Розв'язок нерівності: (2; 3) U (3; +∞)
Д(у) = (2; 3) U (3; +∞).
Відповідь: (2; 3) U (3; +∞)\begin{equation} 9)y=log_{3,1}\frac{|x|+5}{|x|-3} \end{equation} \begin{equation} \frac{|x|+5}{|x|-3}>0 \end{equation} Так, як |x| + 5 > 0 при будь-якому значенні х,
то нерівність буде виконуватися коли |x| - 3 > 0,
тобто |x| > 3, звідки х < -3 і х > 3.
Д(у) = (-∞; -3) U (3; +∞).
Відповідь: (-∞; -3) U (3; +∞)
10) y = logx(2x - x2)
Область визначення задається системою: \begin{equation} \left\{\begin{matrix} x>0 & \\ x\neq 1 & \\ 2x-x^{2}>0 & \end{matrix}\right. \end{equation} \begin{equation} \left\{\begin{matrix} x>0 & \\ x\neq 1 & \\ 0<x<2 & \end{matrix}\right. \end{equation} Розв'яжемо нерівність:
2х - х2 > 0
x(2 - x) > 0
x(2 - x) = 0
x = 0, x = 2

х ∈ (0; 2)
Областю визначення функції
буде розв'язок системи: \begin{equation} \left\{\begin{matrix} x>0 & \\ x\neq 1 & \\ 0<x<2 & \end{matrix}\right. \end{equation}тобто, Д(у) = (0; 1) U (1; 2).
Відповідь: (0; 1) U (1; 2)
11) у = log2x-3(5x - x2)
Область визначення задається системою: \begin{equation} \left\{\begin{matrix} 2x-3>0 & \\ 2x-3\neq 1 & \\ 5x-x^{2}>0 & \end{matrix}\right. \end{equation} \begin{equation} \left\{\begin{matrix} 2x>3 & \\ 2x\neq 4 & \\ x^{2}-5x<0 & \end{matrix}\right. \end{equation} \begin{equation} \left\{\begin{matrix} x>1,5 & \\ x\neq 2 & \\ x(x-5)<0 & \end{matrix}\right. \end{equation} x(x - 5) < 0

Розв'язок нерівності: (0; 5),
отже \begin{equation} \left\{\begin{matrix} x>1,5 & \\ x\neq 2 & \\ 0<x\end{matrix}\right. \end{equation} Отже, область визначення:
Д(у) = (1,5; 2) U (2; 5)
1) y = log11(2x + 6)
2x + 6 > 0
2x > -6 x > -3
Д(у) = (-3; +∞).
Відповідь: (-3; +∞) \begin{equation} 2)y=log_{\frac{1}{6}}(x-3) \end{equation} x - 3 > 0
x > 3
Д(у) = (3; +∞).
Відповідь: (3; +∞) \begin{equation} 3)y=log_{\sqrt{2}}(x^{2}-1) \end{equation} x2 - 1 > 0
x2 - 1 = 0
x2 = 1
x1 = -1, x2 = 1
Д(у) = (-∞; -1) U (1; +∞).
Відповідь: (-∞; -1) U (1; +∞)
4) у = log5,2(3x - x2)
3x - x2 > 0
x2 - 3x < 0
x2 - 3x = 0
x(x - 3) = 0
x1 = 0, x2 = 3

Д(у) = (0; 3).
Відповідь: (0; 3) \begin{equation} 5)y=log_{\frac{3}{8}}(2x^{2}+1) \end{equation} 2x2 + 1 > 0
Нерівність виконується при будь-якому
значення х, отже Д(у) = (-∞; +∞).
Відповідь: R
6) y = logπ(х2 + х + 1)
х2 + х + 1 > 0
Д = 1 - 4 = -3 < 0
Нерівність виконується при будь-якому
значення х, тому Д(у) = (-∞; +∞).
Відповідь: R \begin{equation} 7)y=log_{0,4}\frac{2x-6}{x+2} \end{equation} \begin{equation} \frac{2x-6}{x+2}>0 \end{equation} \begin{equation} \frac{2x-6}{x+2}=0 \end{equation}Нулі чисельника:
2х - 6 = 0
х = 3
Нулі знаменника:
х + 2 = 0
х = -2

Д(у) = (-∞; -2) U (3; +∞).
Відповідь: (-∞; -2) U (3; +ЗБ) \begin{equation} 8)log_{\sqrt{7}}\frac{x^{2}-5x+6}{x-3} \end{equation} \begin{equation} \frac{x^{2}-5x+6}{x-3}>0 \end{equation} \begin{equation} \frac{x^{2}-5x+6}{x-3}=0 \end{equation} Нулі чисельника:
х2 - 5х + 6 = 0
х1 = 2, х2 = 3
Нулі знаменника:
х - 3 = 0
х = 3
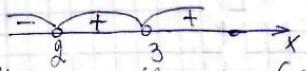
Розв'язок нерівності: (2; 3) U (3; +∞)
Д(у) = (2; 3) U (3; +∞).
Відповідь: (2; 3) U (3; +∞)\begin{equation} 9)y=log_{3,1}\frac{|x|+5}{|x|-3} \end{equation} \begin{equation} \frac{|x|+5}{|x|-3}>0 \end{equation} Так, як |x| + 5 > 0 при будь-якому значенні х,
то нерівність буде виконуватися коли |x| - 3 > 0,
тобто |x| > 3, звідки х < -3 і х > 3.
Д(у) = (-∞; -3) U (3; +∞).
Відповідь: (-∞; -3) U (3; +∞)
10) y = logx(2x - x2)
Область визначення задається системою: \begin{equation} \left\{\begin{matrix} x>0 & \\ x\neq 1 & \\ 2x-x^{2}>0 & \end{matrix}\right. \end{equation} \begin{equation} \left\{\begin{matrix} x>0 & \\ x\neq 1 & \\ 0<x<2 & \end{matrix}\right. \end{equation} Розв'яжемо нерівність:
2х - х2 > 0
x(2 - x) > 0
x(2 - x) = 0
x = 0, x = 2
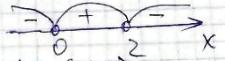
х ∈ (0; 2)
Областю визначення функції
буде розв'язок системи: \begin{equation} \left\{\begin{matrix} x>0 & \\ x\neq 1 & \\ 0<x<2 & \end{matrix}\right. \end{equation}тобто, Д(у) = (0; 1) U (1; 2).
Відповідь: (0; 1) U (1; 2)
11) у = log2x-3(5x - x2)
Область визначення задається системою: \begin{equation} \left\{\begin{matrix} 2x-3>0 & \\ 2x-3\neq 1 & \\ 5x-x^{2}>0 & \end{matrix}\right. \end{equation} \begin{equation} \left\{\begin{matrix} 2x>3 & \\ 2x\neq 4 & \\ x^{2}-5x<0 & \end{matrix}\right. \end{equation} \begin{equation} \left\{\begin{matrix} x>1,5 & \\ x\neq 2 & \\ x(x-5)<0 & \end{matrix}\right. \end{equation} x(x - 5) < 0

Розв'язок нерівності: (0; 5),
отже \begin{equation} \left\{\begin{matrix} x>1,5 & \\ x\neq 2 & \\ 0<x\end{matrix}\right. \end{equation} Отже, область визначення:
Д(у) = (1,5; 2) U (2; 5)
