вправа 4.2.3 гдз 11 клас математика Нелін Долгова 2019

Відповідь ГДЗ:

1) f(x) = e^2x - x
f'(x) = 2e^2x - 1
2e^2x - 1 > 0
2e^2x = 1 \begin{equation} e^{2x}=\frac{1}{2} \end{equation} \begin{equation} ln\frac{1}{2}=2x|:2 \end{equation} \begin{equation} x=\frac{1}{2}ln\frac{1}{2} \end{equation} \begin{equation} x=ln\sqrt{\frac{1}{2}} \end{equation}

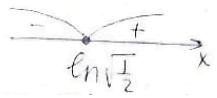
Розв'язок нерівності: \begin{equation} (ln\sqrt{\frac{1}{2}};+\propto ). \end{equation} Відповідь: \begin{equation} (ln\sqrt{\frac{1}{2}};+\propto ) \end{equation} 2) f(x) = 2x - lnx \begin{equation} f'(x)=2-\frac{1}{x} \end{equation} \begin{equation} 2-\frac{1}{x}>0 \end{equation} \begin{equation} \frac{2x-1}{x}>0 \end{equation} Методом інтервалів розв'яжемо нерівність: 
2х - 1 = 0
х = 0,5, х ≠ 0


Отже, х ∈ (-∞; 0) U (0,5; +∞).
Відповідь: (-∞; 0) U (0,5; +∞)
3) f(x) = xlnx f'(x) = x'lnx + x(lnx)' = \begin{equation} =lnx+x\frac{1}{x}= \end{equation} = lnx + 1 lnx + 1 > 0 lnx = -1 \begin{equation} x=e^{-1};x=\frac{1}{e} \end{equation}

Відповідь: \begin{equation} (\frac{1}{e};+\propto ). \end{equation} 4) f(x) = (1 - x)e^-2x
f'(x) = (1 - x)'e^-2x + (1 - x)(e^-2x)' =
= -1 • e^-2x + (1 - x) • (-2) • e^-2x =
= -e^-2x - 2e^-2x + 2xe^-2x =
= 2xe^-2x - 3e^-2x
2xe^-2x - 3e^-2x > 0
e^-2x(2x - 3) > 0
Так, як e^-2x > 0, то нерівність буде виконуватися,
якщо 2x - 3 > 0
2x > 3 x > 1,5.
Відповідь: (1,5; +∞)