Вправа 108 алгебра Істер гдз 9 клас
Задача №108
Умова: Побудуйте графік функції: $$
y=\frac{12-6 x}{x^2-2 x}
$$
Розв'язання:
1. Знайдемо область визначення функції: Знаменник не повинен дорівнювати нулю: $$
x^2-2 x \neq 0
$$
Розв'яжемо рівняння: $$
x(x-2) \neq 0
$$
Звідси: $$
x \neq 0, \quad x \neq 2
$$
Отже, область визначення: $$
D(y): x \in(-\infty ; 0) \cup(0 ; 2) \cup(2 ;+\infty)
$$ 2. Знаходимо вертикальні асимптоти: Функція має розриви в точках $x=0$ і $x=2$.
3. Горизонтальні або похилі асимптоти: Оскільки степінь чисельника менший за степінь знаменника, горизонтальна асимптота: $$
y=0
$$ 4. Перевіримо нулі функції: Чисельник дорівнює нулю: $$
12-6 x=0 \quad \Rightarrow \quad x=2
$$
Проте $x=2$ не входить в область визначення, тому нулів немає.
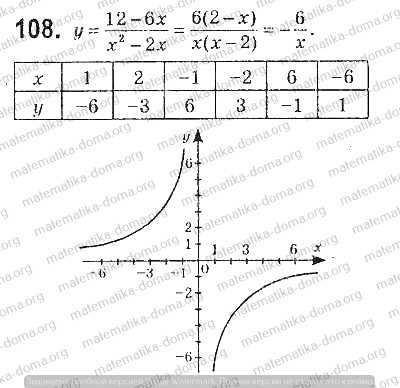
Умова: Побудуйте графік функції: $$
y=\frac{12-6 x}{x^2-2 x}
$$
Розв'язання:
1. Знайдемо область визначення функції: Знаменник не повинен дорівнювати нулю: $$
x^2-2 x \neq 0
$$
Розв'яжемо рівняння: $$
x(x-2) \neq 0
$$
Звідси: $$
x \neq 0, \quad x \neq 2
$$
Отже, область визначення: $$
D(y): x \in(-\infty ; 0) \cup(0 ; 2) \cup(2 ;+\infty)
$$ 2. Знаходимо вертикальні асимптоти: Функція має розриви в точках $x=0$ і $x=2$.
3. Горизонтальні або похилі асимптоти: Оскільки степінь чисельника менший за степінь знаменника, горизонтальна асимптота: $$
y=0
$$ 4. Перевіримо нулі функції: Чисельник дорівнює нулю: $$
12-6 x=0 \quad \Rightarrow \quad x=2
$$
Проте $x=2$ не входить в область визначення, тому нулів немає.










Коментування доступне тільки зареєстрованим
Будь ласка, увійдіть через Google, щоб залишити коментар.