Вправа 602 алгебра Істер гдз 9 клас

Задача №602.
Умова: Побудуйте графік функції та вкажіть їі властивості:
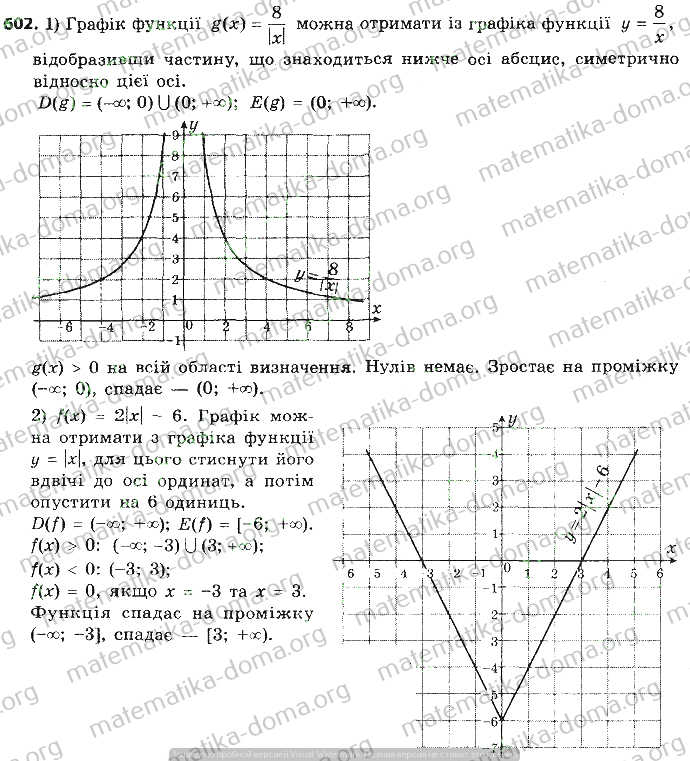
1. $g(x)=\frac{8}{|x|}$;
2. $f(x)=2|x|-6$.

Розв'язання:
1. Функція $g(x)=\frac{8}{|x|}$ :
- Область визначення: $x \neq 0$.
- Парність: Функція парна, оскільки $g(-x)=g(x)$.
- Асимптоти: Вертикальна асимптота при $x=0$.
- Поведінка: $g(x) \rightarrow \infty$ при $x \rightarrow 0 ; g(x) \rightarrow 0$ при $x \rightarrow \infty$.

Графік: Побудуємо.
2. Функція $f(x)=2|x|-6$ :
- Область визначення: $x \in(-\infty,+\infty)$.
- Четність: Функція парна, оскільки $f(-x)=f(x)$.
- Перетин з віссю $y$ :

$$f(0)=2|0|-6=-6$$

- Нулі функції:

$$2|x|-6=0 \Rightarrow|x|=3$$


Тобто, $x=-3$ і $x=3$.
- Зростання та спадання:
- Спадає на інтервалі $(-\infty, 0)$.
- Зростає на інтервалі $(0,+\infty)$.


Відповіді:
1. Функція $g(x)=\frac{8}{|x|}$ :
- Область визначення: $x \in(-\infty, 0) \cup(0,+\infty)$.
- Парність: Парна.
- Асимптоти: Вертикальна при $x=0$.
- Поведінка: $g(x) \rightarrow \infty$ при $x \rightarrow 0 ; g(x) \rightarrow 0$ при $x \rightarrow \infty$.
2. Функція $f(x)=2|x|-6$ :
- Область визначення: $x \in(-\infty,+\infty)$.
- Парність: Парна.
- Перетин з віссю $y: f(0)=-6$.
- Нулі функції: $x=-3$ і $x=3$.
- Зростає на $(0,+\infty)$, спадає на $(-\infty, 0)$.